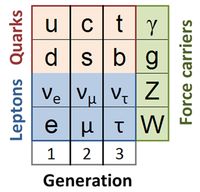
Standard Model
The Standard Model of particle physics is the mathematical theory that describes the weak, electromagnetic and strong interactions between leptons and quarks, the basic particles of particle physics. This model is very strongly supported by experimental observations, and is considered to be a major achievement (perhaps the most outstanding achievement) of theoretical physics. It does not, however, treat the gravitational force, inclusion of which remains an elusive goal of the ultimate "theory of everything". The Standard Model is accordingly not consistent with general relativity. The theory is consistent with special relativity.
The model is described only qualitatively in this article, and neither mathematical details nor experimental phenomenology are provided. The objective here is only an introduction to the basic terminology for particles in the Standard Model and their interactions.
Particles and interactions
Various decay reactions and high-energy interactions between the multitudes of sub-atomic particles (initially just neutrons, protons, electrons, and photons, but extended to observations of pions, kaons, J/ψ's or jay-psi’s, upsilons, and so forth)[1] are well known experimentally, and these facts transcend any theoretical explanation such as the Standard Model. The Standard Model explains these observations through the introduction of fundamental particles: spin 1/2 fermions of two types: leptons and quarks and the forces between them. Fundamental particle interactions are viewed as exchange forces, which is to say the trading back and forth of force carriers, which are different kinds of particle that represent quanta of the underlying force fields. So, for example, the quanta of the electromagnetic field are photons. The strength of an electromagnetic field is dictated by the number of photons that make it up, and the exchange of photons between particles with electric charge is the mechanism underlying the field's ability to exert an electromagnetic force upon these bodies.
Leptons
Leptons are one type of fundamental particle. They have spin 1/2 and are not subject to the strong force. The known leptons are said to be of three families or generations (labeled in the table as 1, 2, 3) and of six flavors, a generic term for the particle names. They are listed in the table below. Their antiparticles also are leptons with opposite electric charge Q and opposite Lepton number Le,μ,τ. For example, the anti-electron or positron has a positive electric charge and a negative electron lepton number Le=−1.
| Particle name | Symbol | Family/Generation | Q (e) | Le | Lμ | Lτ | Mass (MeV) | Lifetime (s) |
|---|---|---|---|---|---|---|---|---|
| Electron | e− | 1 | −1 | +1 | 0 | 0 | 0.510 998 928(11)[2] | Stable |
| Muon | μ− | 2 | −1 | 0 | +1 | 0 | 105.658 3715(35)[3] | 2.197019(21) × 10−6 |
| Tau | τ− | 3 | −1 | 0 | 0 | +1 | 1776.82(16)[4] | 2.906(10) × 10-13 |
| Electron neutrino | νe | 1 | 0 | +1 | 0 | 0 | < 225 × 10−6 [5] | Unknown |
| Muon neutrino | νμ | 2 | 0 | 0 | +1 | 0 | < 0.19 [5] | Unknown |
| Tau neutrino | ντ | 3 | 0 | 0 | 0 | +1 | < 18.2 [5] | Unknown |
The leptons have a weak isospin charge, symbol IW3, related to the weak hypercharge, symbol YW, by:
where Q is the electric charge.
Leptons are classified as right- and left-handed. All the particles in the table exist in a left-handed form and these have a weak hypercharge of YW=−1. The weak isospin charge of a left-handed neutrino is IW3=+1/2 and −1/2 for a left-handed ℓ− lepton. In addition, the electron, muon and tau exist in a right-handed form with Y=−2 and IW3=0. Right-handed neutrinos do not exist. Having a non-zero IW3, only the left-handed leptons couple to the weak interaction.[6][7] Of course, all leptons with electric charge couple to the electromagnetic interaction.
Quarks
Quarks are a type of particle with spin 1/2 that are subject to strong, weak and electromagnetic forces. The known quarks are listed in the table below. The kinds of quark (u, d, c, s, t, d) are referred to as the flavor index of the quark, and besides a flavor index, each quark has a color index, which may be any of three colors: red, green and blue (r, g, b). In a stretched analogy to light, a combination of three quarks with all three colors is referred to as "white" or "colorless" and exhibits no external evidence of a color index. Their antiparticles also are quarks, but carry anti-colors: anti-red, anti-green, anti-blue. A combination of quark and anti-quark with a color and its anti-color is "white" or "colorless".
Unlike a particle's electric charge, which can be any multiple of the elementary charge e, a quark can carry only one unit of color. The elementary unit of color has not been measured, a result of failure to observe an isolated quark.
| Name | Symbol | Family/Generation | B | YW | Q(e) | IS3 | C | S | T | B′ | Mass (MeV) | Antiparticle | Antiparticle symbol |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Up | u | 1 | +1/3 | +1/3 | +2/3 | +1/2 | 0 | 0 | 0 | 0 | 2.34 ± 0.19 [10] | Antiup | ū |
| Down | d | 1 | +1/3 | +1/3 | −1/3 | −1/2 | 0 | 0 | 0 | 0 | 4.78 ± 0.11 [10] | Antidown | |
| Strange | s | 2 | +1/3 | −2/3 | −1/3 | 0 | 0 | −1 | 0 | 0 | 100.2 ± 2.4[10] | Antistrange | |
| Charm | c | 2 | +1/3 | +4/3 | +2/3 | 0 | +1 | 0 | 0 | 0 | 1.294 ± 0.004 × 103 [10] | Anticharm | |
| Bottom | b | 3 | +1/3 | -2/3 | −1/3 | 0 | 0 | 0 | 0 | −1 | 4.19 (+0.18) (−0.06) × 103 [10] | Antibottom | |
| Top | t | 3 | +1/3 | +4/3 | +2/3 | 0 | 0 | 0 | +1 | 0 | 172.9 ±0.6 ±0.9 × 103 [10] | Antitop |
* Notation such as ±xxx denotes measurement uncertainty. In the case of the top quark, the first uncertainty is statistical in nature, and the second is systematic.
The quarks carry fractional electric charge. However, no quark has been observed in isolation, so a "free" fractional electric charge has not been seen.
The quark structure of some strongly interacting sub-atomic particles (some hadrons) is shown in the following tables.[11]
| Name | Symbol | Quark structure | Electric charge | Spin |
|---|---|---|---|---|
| Proton | +1 | 1/2 | ||
| Antiproton | −1 | 1/2 | ||
| Neutron | 0 | 1/2 | ||
| Lambda | 0 | 1/2 | ||
| Omega | −1 | 3/2 |
| Name | Symbol | Quark structure | Electric charge | Spin |
|---|---|---|---|---|
| Pion | +1 | 0 | ||
| Kaon | −1 | 0 | ||
| Rho | +1 | 1 | ||
| D-plus | +1 | 0 | ||
| Eta-c | 0 | 0 |
All baryons must have all three colors present, r, g, and b, and so are colorless, and exhibit no external evidence of the strong color interaction. Likewise, regardless of the flavor combinations in a meson, the colors of the quark-antiquark cancel, so the meson also is colorless to the outside world.[12] The role of the color force is thus simply to hold the quark combinations together, which is accomplished by exchange of gluons among the constituent quarks.
Quanta
Because gravitation is not included in the standard model, there are three type of interaction included. Each type of interaction is mediated by exchange of quanta that are bosons, sometimes called messenger particles.[13]
| Interaction field | Particle name | Symbol | Spin | Range (m) | Mass(GeV) |
|---|---|---|---|---|---|
| Electromagnetic field | Photon | γ | 1 | ∞ | < 10−27 [14] |
| Weak field | Weak bosons | W+, W−, Z | 1 | ≈ 10−17 | MW=80.399±0.023;[15] MZ=91.1876±0.0021[16] |
| Strong field | Gluons (8) | g | 1 | ≈ 10−15 | 0[17] |
Photons
The photon mediates the electromagnetic force and has a very long history. It has neither electric charge nor mass. See the article Quantization of the electromagnetic field.
Weak gauge bosons
The massive W+, W−, Z, weak bosons are the messenger particles for the weak force. Their nonzero mass is expected from the Standard Model because of the introduction of the Higgs boson, a particle with a mass of 125 GeV first observed in 2012 at CERN.[18] The W+, W− are antiparticles of each other and the Z boson is its own antiparticle.
Gluons
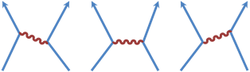
Gluons mediate the strong force as an exchange force due to color, one property of quarks. A gluon carries both a color and an anti-color. When a quark emits a gluon, its color changes in a way dependent upon the color/anti-color of the emitted gluon. For example, a red quark can emit a red-antiblue gluon, becoming a blue quark. There are nine possible color-anticolor combinations of r, g, b, which leads to only eight possible gluons because emission by a quark of one color-anticolor combination doesn't change the state of a quark and cannot act as a messenger.[19] The remaining eight gluon color combinations are shown below.[18]
The peculiar combinations: , , result from arranging all the possible combinations of colors and anti-colors as symmetrized unit vectors in a space of color/anti-color products.
The color force has a complex behavior. At large momenta and short distances the quark-gluon coupling is weak and it is found that one can probe the inside of a hadron with high-energy probes to see the consequences of "quasi-free" quarks in this regime of "asymptotic freedom". In the contrasting case of low momenta, the quark-gluon interaction gains strength and for energies below (approximately) 0.5 GeV the isolation of quarks is impossible, and they exist only in complexes, a phenomenon called "quantum confinement".[20]
Nuclear forces and mesons
The interpretation of nuclear forces based upon the Standard Model and the quarks is described in the article Nuclear force.
What is missing?
The Standard Model enables calculations related to observations of elementary particles and their reactions. However, it does so based upon a number of entirely non-intuitive postulates about the symmetries of nature, and based upon a host of empirical parameters whose values are not explained. Among these parameters are the masses of the elementary particles and the coupling constants for the field strengths. The Standard Model combines the weak and electromagnetic forces as the electroweak force, but the electroweak and strong forces act independently, so they are not truly unified as aspects of a single force. Also, the Standard Model leaves open how gravity is to be included. A more complete and less arbitrary theory is the goal of a "grand unified theory", such as string theory and quantum gravity, among others.[21][22]
References
- ↑ For an introduction, see Lincoln Wolfenstein, Joao P. Silva (2010). “Chapter 5: The birth of particle physics”, Exploring Fundamental Particles. Taylor & Francis, pp. 47 ff. ISBN 1439836124.
- ↑ Electron mass energy equivalent in MeV mec02. NIST. Retrieved on 2011-08-26.
- ↑ Muon mass energy equivalent in MeV mμc02. NIST. Retrieved on 2011-08-26.
- ↑ Tau mass energy equivalent in MeV mτc02. NIST. Retrieved on 2011-08-26.
- ↑ Jump up to: 5.0 5.1 5.2 K. Nakamura et al. (June 16, 2011). Neutrino properties. PDG Particle listings. Particle Data Group.
- ↑ Alessandro Bettini (2008). Introduction to elementary particle physics. Cambridge University Press, p. 305. ISBN 0521880211.
- ↑ HG Dosch (2007). Ion-Olimpiu Stamatescu, Erhard Seiler, eds: Approaches to fundamental physics: an assessment of current theoretical ideas. Springer, p. 34. ISBN 3540711155.
- ↑ Ajay K. Saxena (2005). “Table 18.13: The six quarks and their corresponding quantum numbers”, Principles of modern physics. Alpha Science Int'l Ltd.. ISBN 1842652133.
- ↑ Michael Mansfield, Colm O'Sullivan (2011). “Table 22.5: Quark properies”, Understanding Physics, 2nd ed. John Wiley and Sons, p. 615. ISBN 1439048398.
- ↑ Jump up to: 10.0 10.1 10.2 10.3 10.4 10.5 K. Nakamura et al. (January 15, 2011). QUARKS. PDG Particle listings. Particle Data Group.
- ↑ Information for tables from Tai L. Chow (2008). “Tables 9.3 and 9.4”, Gravity, black holes, and the very early universe: an introduction to general relativity and cosmology. Springer, p. 168. ISBN 0387736298.
- ↑ Brian J. McParland (2010). Nuclear Medicine Radiation Dosimetry: Advanced Theoretical Principles. Springer, p. 36. ISBN 1848821255.
- ↑ Britannica Educational Publishing (2011). “The basic forces and their messenger particles”, Erik Gregersen, ed: The Britannica Guide to Particle Physics. The Rosen Publishing Group, p. 15. ISBN 1615303820.
- ↑ K. Nakamura et al. (June 16, 2011). γ. PDG Particle listings. Particle Data Group.
- ↑ K. Nakamura et al. (June 16, 2011). W. PDG Particle listings. Particle Data Group.
- ↑ K. Nakamura et al. (June 16, 2011). Z. PDG Particle listings. Particle Data Group.
- ↑ K. Nakamura et al. (June 16, 2011). g or gluon. PDG Particle listings. Particle Data Group.
- ↑ Jump up to: 18.0 18.1 Andrew Watson (2004). “Table 4.4: The eight gluon color configurations”, The quantum quark. Cambridge University Press, p. 175. ISBN 0521829070.
- ↑ O. M. Boyarkin, Alfred L. Heinzerton (2007). Introduction to Physics of Elementary Particles. Nova Publishers, p. 2. ISBN 160021200X.
- ↑ Kerson Huang (1992). Quarks, leptons & gauge fields, 2nd ed. World Scientific, pp. 9-10. ISBN 9810206593.
- ↑ Stephen Hawking, Leonard Mlodinow (2010). “Chapter 5: The theory of everything”, The Grand Design. Bantam, p. 112. ISBN 0553805371.
- ↑ Peter Woit (2006). “Chapter 8: Problems of the Standard Model”, Not even wrong: the failure of string theory and the search for unity in physical law. Basic Books, pp. 91 ff. ISBN 0465092756.