Logarithm: Difference between revisions
imported>Fredrik Johansson (fix markup; correction) |
imported>Fredrik Johansson (markup) |
||
| Line 1: | Line 1: | ||
A '''logarithm''' is a mathematical function which provides the number which would appear as the exponent in an expression. For example, since <math>343 = 7^3</math>, then the base-7 logarithmic function of 343 is 3. In general, if <math>a = b^c</math>, then <math>log_b(a) = c</math>. | A '''logarithm''' is a mathematical function which provides the number which would appear as the exponent in an expression. For example, since <math>343 = 7^3</math>, then the base-7 logarithmic function of 343 is 3. In general, if <math>a = b^c</math>, then <math>\log_b(a) = c</math>. | ||
Because we use a base-10 number system, it is often convenient to use 10 as the base of the logarithm. Multiplying a number by 10 appends a zero to the numeral and adds 1 to the logarithm. For example, <math>log_{10}(43)</math> is approximately equal to 1.63347, and multiplying by 10, <math>log_{10}(430)</math> is approximately 2.63347. | Because we use a base-10 number system, it is often convenient to use 10 as the base of the logarithm. Multiplying a number by 10 appends a zero to the numeral and adds 1 to the logarithm. For example, <math>\log_{10}(43)</math> is approximately equal to 1.63347, and multiplying by 10, <math>\log_{10}(430)</math> is approximately 2.63347. | ||
Mathematicians and physicists often find, however, that the transcendental number <math>e</math> is more convenient as a base for a logarithmic function. The value of <math>e</math> is approximately equal to 2.718281828459045. The logarithmic function with <math>e</math> as a base is called the "natural logarithm" and is written <math>ln(x)</math>. | Mathematicians and physicists often find, however, that the transcendental number <math>e</math> is more convenient as a base for a logarithmic function. The value of <math>e</math> is approximately equal to 2.718281828459045. The logarithmic function with <math>e</math> as a base is called the "natural logarithm" and is written <math>\ln(x)</math>. | ||
The natural logarithm function <math>\ln(x)</math> is the [[integral]] of the function <math>f(x) = \frac{1}{x}</math>. | The natural logarithm function <math>\ln(x)</math> is the [[integral]] of the function <math>f(x) = \frac{1}{x}</math>. | ||
| Line 21: | Line 21: | ||
:<math>10^{-3} = \frac{1}{10^3}</math> | :<math>10^{-3} = \frac{1}{10^3}</math> | ||
and it then follows that | and it then follows that | ||
:<math>log_{10}(0.001) = -3</math>. | :<math>\log_{10}(0.001) = -3</math>. | ||
Thus, logarithms of numbers between 0 and 1 are negative numbers, and logarithms of numbers that fall between powers of the base are non-integer real numbers. | Thus, logarithms of numbers between 0 and 1 are negative numbers, and logarithms of numbers that fall between powers of the base are non-integer real numbers. | ||
| Line 27: | Line 27: | ||
== Shape of the logarithm function == | == Shape of the logarithm function == | ||
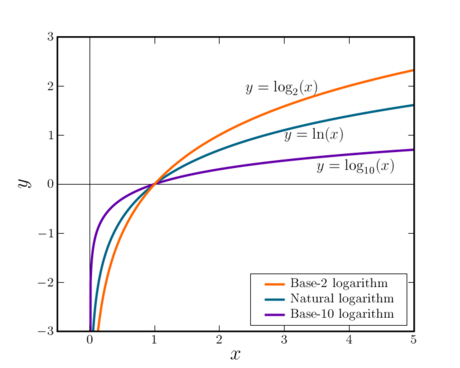
Consider the function <math>f(x) = log_b(x)</math> where b is a positive real-number base of the logarithm. Since any positive real number raised to the exponent zero is 1, the logarithm of 1 is zero. To the right of 1 on the x-axis, the function <math>f</math> continually increases, but increases more and more slowly as <math>x</math> heads towards infinity. Between 1 and 0, the logarithmic function has negative values, and asymptotically approaches minus infinity as <math>x</math> approaches zero. For negative values of <math>x</math>, there is no defined value of <math>f(x)</math> within the real numbers — but using complex numbers a value can be found, as will be discussed further below. | Consider the function <math>f(x) = \log_b(x)</math> where b is a positive real-number base of the logarithm. Since any positive real number raised to the exponent zero is 1, the logarithm of 1 is zero. To the right of 1 on the x-axis, the function <math>f</math> continually increases, but increases more and more slowly as <math>x</math> heads towards infinity. Between 1 and 0, the logarithmic function has negative values, and asymptotically approaches minus infinity as <math>x</math> approaches zero. For negative values of <math>x</math>, there is no defined value of <math>f(x)</math> within the real numbers — but using complex numbers a value can be found, as will be discussed further below. | ||
[[Image:Logarithms.png|460px|center|]] | [[Image:Logarithms.png|460px|center|]] | ||
| Line 34: | Line 34: | ||
Suppose we know the logarithm of a number using one base <math>b</math>, and we want to find the logarithm using a different base <math>c</math> : | Suppose we know the logarithm of a number using one base <math>b</math>, and we want to find the logarithm using a different base <math>c</math> : | ||
:<math>log_b(x) = y</math> | :<math>\log_b(x) = y</math> | ||
:<math>log_c(x) = </math>? | :<math>\log_c(x) = </math>? | ||
Suppose we know <math>y</math>, <math>b</math> and <math>c</math> and we want to find <math>log_c(x)</math>. | Suppose we know <math>y</math>, <math>b</math> and <math>c</math> and we want to find <math>\log_c(x)</math>. | ||
We need to look up the value of <math>log_c(b)</math>, and then by multiplying we can find the desired quantity : | We need to look up the value of <math>\log_c(b)</math>, and then by multiplying we can find the desired quantity: | ||
:<math>log_c(x) = log_c(b)log_b(x) </math> | :<math>\log_c(x) = \log_c(b)\log_b(x) </math> | ||
This formula can be established using the definition of logarithms and the rule for multiplying exponents : | This formula can be established using the definition of logarithms and the rule for multiplying exponents: | ||
:<math>x = b^{log_bx}</math> | :<math>x = b^{\log_bx}</math> | ||
:<math>b = c^{log_cb}</math> | :<math>b = c^{\log_cb}</math> | ||
:<math>x = (c^{log_cb})^{log_bx}</math> | :<math>x = (c^{\log_cb})^{\log_bx}</math> | ||
:<math>x = c^{log_c(b) log_b(x)}</math> | :<math>x = c^{\log_c(b) \log_b(x)}</math> | ||
Therefore <math>log_c(x) = log_c(b)log_b(x) </math>, the formula we wished to prove. | Therefore <math>\log_c(x) = \log_c(b)\log_b(x) </math>, the formula we wished to prove. | ||
A useful formula for <math>log(xy)</math> can be derived using the rule for adding exponents : | A useful formula for <math>\log(xy)</math> can be derived using the rule for adding exponents: | ||
:<math>b^{log_b(xy)} = xy = b^{log_bx}b^{log_by} = b^{log_bx + log_by}</math> | :<math>b^{\log_b(xy)} = xy = b^{\log_bx}b^{\log_by} = b^{\log_bx + \log_by}</math> | ||
Therefore : | Therefore : | ||
:<math>log_b(xy) = log_b(x) + log_b(y)</math> | :<math>\log_b(xy) = \log_b(x) + \log_b(y)</math> | ||
==Complex numbers and logarithms == | ==Complex numbers and logarithms == | ||
The exponential function of an imaginary number is given as | The exponential function of an imaginary number is given as | ||
:<math>e^{ix} = cos(x) + | :<math>e^{ix} = \cos(x) + i\sin(x)</math> | ||
To find the logarithm of a complex number <math>a + bi</math>, | To find the logarithm of a complex number <math>a + bi</math>, it's convenient to express the number in polar coordinates <math>(r,\theta)</math> where <math>r = \sqrt{a^2 + b^2}</math> and <math>\theta = \arctan(\frac{b}{a})</math> (Intuitively, <math>r</math> is the length of the line segment joining the number to the origin in the complex plane, and <math>\theta</math> is the angle that line segment makes with the <math>x</math>-axis.) The equivalence of the two notations is given by | ||
:<math>a + bi = r(cos(\theta) + i sin(\theta))</math>. | :<math>a + bi = r(\cos(\theta) + i \sin(\theta))</math>. | ||
Suppose we define <math>c + di</math> such that <math>ln(a + bi) = c + di</math>. Using the formula for the exponential function above, | Suppose we define <math>c + di</math> such that <math>\ln(a + bi) = c + di</math>. Using the formula for the exponential function above, | ||
:<math>a + bi = e^{c + di} = e^ce^{di} = e^c(cos(d) + i sin(d))</math> | :<math>a + bi = e^{c + di} = e^ce^{di} = e^c(\cos(d) + i \sin(d))</math> | ||
It can be seen from similarity with the above formula for polar coordinates that <math> r = e^c</math> and <math>d = \theta</math>. | It can be seen from similarity with the above formula for polar coordinates that <math> r = e^c</math> and <math>d = \theta</math>. | ||
Therefore : | Therefore : | ||
:<math>ln(a + bi) = c + di = ln( r ) + i \theta = ln(\sqrt{a^2 + b^2}) + i arctan(\frac{b}{a})</math>. | :<math>\ln(a + bi) = c + di = \ln( r ) + i \theta = \ln(\sqrt{a^2 + b^2}) + i \arctan(\frac{b}{a})</math>. | ||
In this way, the logarithmic function can be extended to cover the entire complex plane except for the number zero, which has an undefined value — a singularity with the real part heading towards minus infinity and the imaginary part spinning wildly. | In this way, the logarithmic function can be extended to cover the entire complex plane except for the number zero, which has an undefined value — a singularity with the real part heading towards minus infinity and the imaginary part spinning wildly. | ||
Revision as of 17:57, 28 April 2007
A logarithm is a mathematical function which provides the number which would appear as the exponent in an expression. For example, since , then the base-7 logarithmic function of 343 is 3. In general, if , then .
Because we use a base-10 number system, it is often convenient to use 10 as the base of the logarithm. Multiplying a number by 10 appends a zero to the numeral and adds 1 to the logarithm. For example, is approximately equal to 1.63347, and multiplying by 10, is approximately 2.63347.
Mathematicians and physicists often find, however, that the transcendental number is more convenient as a base for a logarithmic function. The value of is approximately equal to 2.718281828459045. The logarithmic function with as a base is called the "natural logarithm" and is written .
The natural logarithm function is the integral of the function .
Extension of logarithms to fractional and negative values
Originally, exponents were natural numbers: it's easy to see the meaning of an expression such as . Rules for adding and multiplying exponents were noticed, and to extend the idea to fractions and negative numbers it was assumed that the same rules would apply. To define a meaning for a fractional value such as , consider that, using a rule for multiplying exponents,
Therefore must be and this then supplies a value for . Values for many other numbers can be worked out similarly using cube roots and so on, and values for all real numbers can then be defined using limits.
To assign meaning to negative values of exponents, note the rule that
- .
So, for example, to find the meaning of , consider
Therefore,
and it then follows that
- .
Thus, logarithms of numbers between 0 and 1 are negative numbers, and logarithms of numbers that fall between powers of the base are non-integer real numbers.
Shape of the logarithm function
Consider the function where b is a positive real-number base of the logarithm. Since any positive real number raised to the exponent zero is 1, the logarithm of 1 is zero. To the right of 1 on the x-axis, the function continually increases, but increases more and more slowly as heads towards infinity. Between 1 and 0, the logarithmic function has negative values, and asymptotically approaches minus infinity as approaches zero. For negative values of , there is no defined value of within the real numbers — but using complex numbers a value can be found, as will be discussed further below.
Manipulating logarithms
Suppose we know the logarithm of a number using one base , and we want to find the logarithm using a different base :
- ?
Suppose we know , and and we want to find . We need to look up the value of , and then by multiplying we can find the desired quantity:
This formula can be established using the definition of logarithms and the rule for multiplying exponents:
Therefore , the formula we wished to prove.
A useful formula for can be derived using the rule for adding exponents:
Therefore :
Complex numbers and logarithms
The exponential function of an imaginary number is given as
To find the logarithm of a complex number , it's convenient to express the number in polar coordinates where and (Intuitively, is the length of the line segment joining the number to the origin in the complex plane, and is the angle that line segment makes with the -axis.) The equivalence of the two notations is given by
- .
Suppose we define such that . Using the formula for the exponential function above,
It can be seen from similarity with the above formula for polar coordinates that and .
Therefore :
- .
In this way, the logarithmic function can be extended to cover the entire complex plane except for the number zero, which has an undefined value — a singularity with the real part heading towards minus infinity and the imaginary part spinning wildly.