Fenske equation: Difference between revisions
imported>Milton Beychok m (Revised some CZ links) |
imported>Milton Beychok m (Fixed typo) |
||
| Line 2: | Line 2: | ||
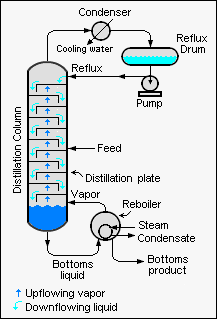
[[Image:Total Reflux.png|thumb|right|275px|{{#ifexist:Template:Total Reflux.png/credit|{{Total Reflux.png/credit}}<br/>|}}Industrial distillation column operating at total reflux]] | [[Image:Total Reflux.png|thumb|right|275px|{{#ifexist:Template:Total Reflux.png/credit|{{Total Reflux.png/credit}}<br/>|}}Industrial distillation column operating at total reflux]] | ||
The '''Fenske equation''' is used for calculating the minimum number of [[theoretical | The '''Fenske equation''' is used for calculating the minimum number of [[theoretical plate]]s required for the separation of a binary feed stream by a [[Continuous distillation|distillation column]] that is being operated at total [[Continuous distillation|reflux]] (i.e., which means that no overhead product is being withdrawn from the column). The derivation of the Fenske equation assumes that the [[relative volatility]] is constant in the distillation column. | ||
Theoretical plates are also often referred to as [[theoretical tray]]s or [[equilibrium stage]]s. | Theoretical plates are also often referred to as [[theoretical tray]]s or [[equilibrium stage]]s. | ||
Revision as of 11:17, 1 August 2008
The Fenske equation is used for calculating the minimum number of theoretical plates required for the separation of a binary feed stream by a distillation column that is being operated at total reflux (i.e., which means that no overhead product is being withdrawn from the column). The derivation of the Fenske equation assumes that the relative volatility is constant in the distillation column.
Theoretical plates are also often referred to as theoretical trays or equilibrium stages.
The equation was derived by Merrell Fenske in 1932 [1], a professor who served as the head of the chemical engineering department at the Pennsylvania State University from 1959 to 1969.
A common version of the Fenske equation
This is one of the many different but equivalent versions of the Fenske equation:[2][3][4][5]
where:
| = minimum number of theoretical plates required at total reflux (of which the reboiler is one) | |
| = mole fraction of more volatile component in the overhead distillate | |
| = mole fraction of more volatile component in the bottoms product | |
| = average relative volatility of more volatile component to less volatile component |
For ease of expression, the more volatile and the less volatile components are commonly referred to as the light key (LK) and the heavy key (HK), respectively.
If the relative volatility of the light key to the heavy key is constant from the column top to the column bottom, then is simply . If the relative volatility is not constant from top to bottom of the column, then the following approximation may be used:[2]
| where: | |
| = relative volatility of light key to heavy key at the top of the column | |
| = relative volatility of light key to heavy key at the bottom of the column |
The above form of the Fenske equation can be modified for use in the total reflux distillation of multi-component feeds.[3]
Another form of the Fenske equation
A derivation of another form of the Fenske equation for use in gas chromatography is available on the U.S. Naval Academy's web site.[6] Using Raoult's law and Dalton's Law for a series of condensation and evaporation cycles (i.e., equilibrium stages), the following form of the Fenske equation is obtained:
| where: | |
| = number of equilibrium stages | |
| = mole fraction of component n in the vapor phase | |
| = mole fraction of component n in the liquid phase | |
| = vapor pressure of pure component n |
Shortcut calculations for designing distillation columns
There are many so-called shortcut calculation methods for designing industrial distillation columns. The most commonly used one is the Fenske-Underwood-Gilliland method.
The Fenske equation estimates the minimum number of theoretical plates or equilibrium stages at total reflux. The Underwood equation[7] estimates the minimum reflux for an infinite number of theoretical equilibrium stages. The Gilliland method[8] then uses Fenske's minimum plates and Underwood's minimum reflux to estimate the theoretical plates for a given distillation at a chosen reflux.
The estimates such as provided by the Fenske-Underwood-Gilliland shortcut calculations are most effective when used to obtain a preliminary design before following up with the use of distillation simulation software which utilize much more rigorous calculation methods.
References
- ↑ Fenske, M.R. (1932). Industrial Engineering Chemistry, Vol. 24: 482.
- ↑ 2.0 2.1 Distillation notes (Loren Schreiber, Florida State University)
- ↑ 3.0 3.1 Lecture 13: Fenske Equation (Queens University, Canada)
- ↑ Tutorial 6: Separation Processes (J. Skilling, University of Edinburgh, Scotland)
- ↑ Maxwell, J.B. (1950). Data Book on Hydrocarbons, 1st Edition. D. Van Nostrand.
- ↑ Fenske Equation (U.S. Naval Academy)
- ↑ A.J.V. Underwood (1948). Chemical Engineering Progress, Vol. 4:603.
- ↑ E.R. Gilliland (1940). Industrial Engineering Chemistry, Vol.32:1220.
![{\displaystyle \ N={\frac {\log \,{\bigg [}{\Big (}{\frac {X_{d}}{1-X_{d}}}{\Big )}{\Big (}{\frac {1-X_{b}}{X_{b}}}{\Big )}{\bigg ]}}{\log \,\alpha _{avg}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06af3d7fcd0e4cac0751fb951d065cca1c4fcaf5)












