User:Dmitrii Kouznetsov/Analytic Tetration

Fig.0. Graphic of analytic tetration $f=F_{2}(x)=\exp _{2}^{x}(1)$ at versus $x$.

Abstract

Analytic tetration is defined as mathematical function that coincides witht the tetration at integer values of the argument and is analytic outside the negative part of the real axis. Existence of such a function is postulated; and arguments in favor of uniqueness of such a function are considered. The algorithm of evaluation is suggested. Examples of evaluation, pictures and tables are supplied. The application and the generalization is discussed.

Preface

The colleagues indicated so many misprints in my papers about tetration, posted at my homepage , that I want to give them opportunity to correct them in real time.

Especially I invite

• Arthur Knoebel
• Henryk Trappman
• Andrew Robbins

to edit this file.

I consider the topic very important and urgent. The analytic tetration should be investigated and discussed right now; overvice, the non-analytic extension may become an ugly standard in mathematics of computation; the implementation of hige numbers with non-analytic tetration would make difficult realization of arithmetic operations and cause a lot of incompatibilities.

This is my apology for posting this research now, while the rigorous proof of existence and uniqueness of the analytic tetration is not yet found. My believe is based on the numerical check of the hypothesis of the existence and uniqueness, on smallness of the residual at the substitution of the function to the tetration equation and beauty of the resulting pictures. I cannot imagine that the agreement with 14 decimal digits occurs just by occasion without deep mathematical meaning.

In such a way I apologize for postulating of statements which should be prooven by the rigorous mathematical deduction.

Introduction

Quick start

Roughly, super-exponential

(1) $F_{b}(z)=\exp _{b}^{z}(1)$

is combination of $x$ exponentials on base $b$. For example,

$~F_{b}(0)=\exp _{b}^{0}(1)=1$

$~F_{b}(1)=\exp _{b}(1)=b$

$~F_{b}(2)=\exp _{b}^{2}(1)=\exp _{b}(\exp _{b}(1))=b^{b}$

$~F_{b}(3)=\exp _{b}^{3}(1)=\exp _{b}{\Big (}\exp _{b}{\big (}\exp _{b}(1){\big )}{\Big )}=b^{b^{b}}$

and so on. However, such definition is good only for positive integer values of $x$. In general, the superexponential can be defined through the Abel equation

(2) $~\exp _{b}{\Big (}F_{b}(z){\Big )}=F_{b}(z+1)$

with additional condition that

(3) $~F_{b}(0)=1$

Then, at least for positive values of $~b$ and positive integer values of $~z$, such a definition can be used for the evaluation of tetration.

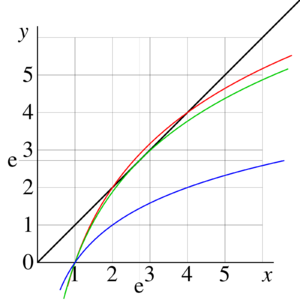
In this paper, the way to define tetration for non-integer argument is described. For real values of the argument, at $~b=2$, such a tetration is plotted on figure 0. In the following sections, I describe, why is it so important, how to define the tetration for non-integer values of the argument, how can it be evaluated with high precision and why it is the only correct way to define analytic tetration.

Additional argument

One can consider to add the additional argument, replacing $~\exp _{b}(1)$ to $~\exp _{b}(a)$. This may have sense, while $~z$ is allowed to have only integer values. However, at the implementation of "good" tetration, the "argument" $~a$ can be considered as inverse superexponential of some argument, $~a=F_{b}(\alpha )$; then, $~\exp _{b}^{z}(a)=F_{b}{\Big (}F_{b}(\alpha ){\Big )}$; in the way, similar to that of convential logarithms: it is sufficient to investigate properties of natural logarithm ln; then, any other can be expressed as $\log _{b}(z)=\ln(z)/\ln(b)$.

$\exp _{b}^{n}(\exp _{b}^{m}(z))=\exp _{b}^{m+n}(z)$

The exponentiation of tetration is equivalent to increment of its argument. While summaton operation forms the group, exponentiation does too.

$\exp _{b}^{m}(F_{b}(z))=F_{b}(z+m)$

Inverse function and group properties

In this section, I write $~F$ instead of $~F_{b}$ and $~\exp(z)$ instead of $~\exp _{b}(z)$; onitting indices. However, you may recover them at any moment.

(I am not sure which notation is best. D.)

The speculation of the previous subseciton can be written shorter.

Assume there exist function $~F^{-1}$ such that $~F{\Big (}F^{-1}(z){\Big )}=z$.

Let $~s=\exp ^{u}(t)=F{\Big (}u+F^{-1}(t){\big )}$ and $~q=\exp ^{v}(s)=F{\Big (}v+F^{-1}(s){\big )}$ .

Then $~q=\exp ^{v}{\Big (}\exp ^{u}(t){\Big )}=F{\Big (}v+F^{-1}{\Big (}F(u+F^{-1}(t)){\Big )}{\Big )}=F{\Big (}v+u+F^{-1}(t){\Big )}$.

You can put subscript $~_{b}$ to $~F$ and $~\exp$ in the defuction above, and it will be seen, that we have no need to deal with funciton of 2 variables, considering $\exp _{b}^{z}(x)$; it can be expressed in terms of $F_{b}(z)$. However, we need to specify, what set shold be $~t$ and $~s$ from in the deduction above: must they be positive integer, or they can be real, of they can be also complex numbers.

History of tetration and huge numbers

Perhaps, every researcher used to see diagnostivs "floating overflow" at the evlauation of an expression with huge numbers....

Asymptotic

Assume, the tetration $F$ is defined with the Abel equation

(10) $\exp _{b}(F(z))=F(z+1)$

and assume the condition

(11) $F(0)=1$

While one deal with real axis, one imagine some real-analytic extension shown in Figure 0 and consider also

(12) $G(z)=F(z+k(z))$

where

(13) $k(z)=\sum _{n=-\infty }^{\infty }\alpha _{n}\exp(2\pi {\rm {i}}nz)$

Such a funciton is also coluiton of the Abel equation; at

(14) $\alpha _{-n}=(\alpha _{n})^{*}$

and

(15) $\alpha _{0}=-\sum _{n\neq 0}\alpha _{n}$

function $~G$ is real and passes through the same points as </math>~F</math> at integer values of the argument.

and at small values of coefficients $\alpha$, function $~G$ looks smooth, and it is difficult to guess, which of them is "true". For this reason, for the standard mathematical representation, the non-analytic stepwice funciton uxp was suggested .

However, the difference between functions $~F$ and $~G$ nefomes seen, if one of them, for example, $~F$, is analytic and regular in the upper and lower half-planes; function $~G(z)$ will be analytic only within the strip $~|z|<y_{0}$; order of magnitude of $~y_{0}$ can be estimated with

$y_{0}\approx {\rm {MIN}}_{n}~{\frac {\ln(2/|\alpha _{n}|)}{2\pi n}}$

At larger values of the imaginary part of the arguemnt, the periodic function $k$ takes huge values, including various negative integers. Namely at these values, function $~F$ has singulatities.

For abstract excersize in comlex functional analysis,all animals are equal. However, for the applicaitons in the computaional mathematics, some of them are more equal than other. As such a more equal animal we should choose the function with simplest behavior, with minimum of singulatities, and easiest for the evaluation.

Eigenvalues of logarithm

FIg.1. Example of graphic solution of equation $L=\log _{b}(L)$ for $b={\sqrt {2}}$ (two real solutions, $L=2$ and $L=4$), $b=\exp(1/{\rm {e)}}$ (one real solution $L={\rm {e}}$) $b=2$ (no real solutions).

Function $F$ is supposed to grow up (faster than any exponential) in the direction of the real axis, at least for $b>\exp(1/{\rm {e)}}$, However, it has no need to grow in other directions: neither in the negative direction of the real axis, nor in the direction of the imaginary axis.

For computational mathematics, it would be better, if the funciton $F$ does not grow at all, approaching some limiting value. Also, for computation, it would be better, if all the signulatities of function $~F$ are at the real axis; at values $-2$ and less (more negative).

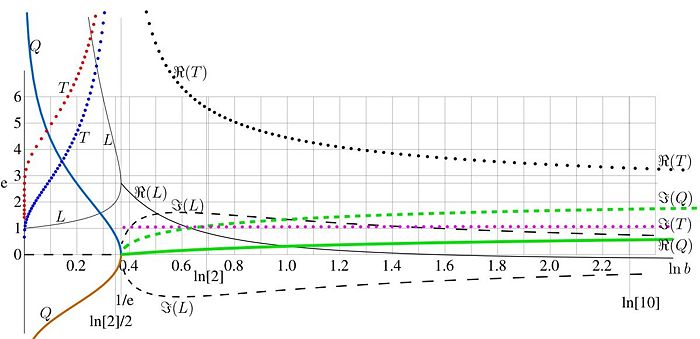
There are not so many options in choise of the limiting value. From the equaiton of Abel, it follows, that the asymptotics should be eigenvalue of logarithm, i.e., solution $~L$ of equation

(20) $L=\log _{b}(L)$

Figure 1 shows the graphic of the left-hand side the of this equation (black line) and 3 examples of the right-hand side.

Two real solutions exist at $~b<\exp(1/{\rm {e)}}$. These solutions are plotted versus $~\ln(b)$ in Figure 2 with thin black solid line.

One real solution $~L={\rm {e}}$ exists at $~b=\exp(1/{\rm {e)}}$.

Two complex solutions exist at $~b>\exp(1/{\rm {e)}}$. These solutions are mutially conjugated. The real part is plotted with solid line, and two options for the imaginary part are plotted with dashed line.

FIg.2. parameters of asymptotic of tetration versus logarithm of the base

Exponential asymptotic

Consider tetration with following asymptotic behavior:

(30) $F(z)=L+\exp(Qz+r)+o{\Big (}\exp(Qz+r){\Big )}$

where $~Q$ has sense of increment and $~r$ determines the amplutude and phase of the wave, exponentially growing from the small values.

Possible values of $~Q$ are plotted versus $~\ln(b)$ in FIgure 2 with thick lines.

Quasi-period $T=2\pi /Q$ is plotted with dotted lines.

At small base, both values of quasiperiod are pure imaginary. This periodic or quasi-periodic behavior is similar to that of the conventional exponential, but function $~F$ does not grow to infinity in the direction of the real axis, aproaching eigenvalue $L$ of logarithm. One example of such a behavior $~b={\sqrt {2}}$ is shown in Figure 3 for $~b={\sqrt {2}}$. The following section describes, how it was ploted.

At $~b>\exp(1/{\rm {e}})$ values of period $T$ are complex; and $\Re (T)>0$. This corresponds to the exponential growth of the asymptotic solution in the direction of the real axis; at large positive values of $\Re (Qz)$ the asymptotic does not approximate the function which grows faster than any exponential.

Small base. Base $b={\sqrt {2}}$

Fig.3. Tetration $f=F(z)$ at the complex $z$-plane. Levels of integer $\Re (f)$ and levels of integer $\Im (f)$ are shown with thick lines. Grid covers with unit step range ($-10\leq \Re (z)\leq 10$, $-10\leq \Im (z)\leq 10$).

For evaluation of Tetration we need to assume that it exists, and has asymptotic (30).

Consider the case of $1<b<\exp(1/{\rm {e)}}$. at fixed values of real part of the argument, the function has periodic behavior in the direction of imaginary axis, as it is shown in Fig. 3. In this figure, the example with $b={\sqrt {2}}$ is used. Function is periodic; period $T\approx 17.1431~{\rm {i}}$.

As all analytic tetrations, function has limiting values;

$\lim _{x\rightarrow \infty }F_{\sqrt {2}}(x+{\rm {i}}y)=2$

$\lim _{x\rightarrow -\infty }F_{\sqrt {2}}(x+{\rm {i}}y)=4$

At non-zero values of the imaginary part of the argument, the function decays to these asymptotiv values.

At the real axis, the $~F(z)$ has cut at $z\leq -2$.

Due to the periodicity, the function has cuts also at

$Z+Tn\leq -2$ for integer $~n$.

As all other tetrations, it has singularity at $z=-2$, $~F(-1)=0$ and $~F(0)=1$.

Other, more singular tetrations can be obtained by light periodic deformation of the argument.

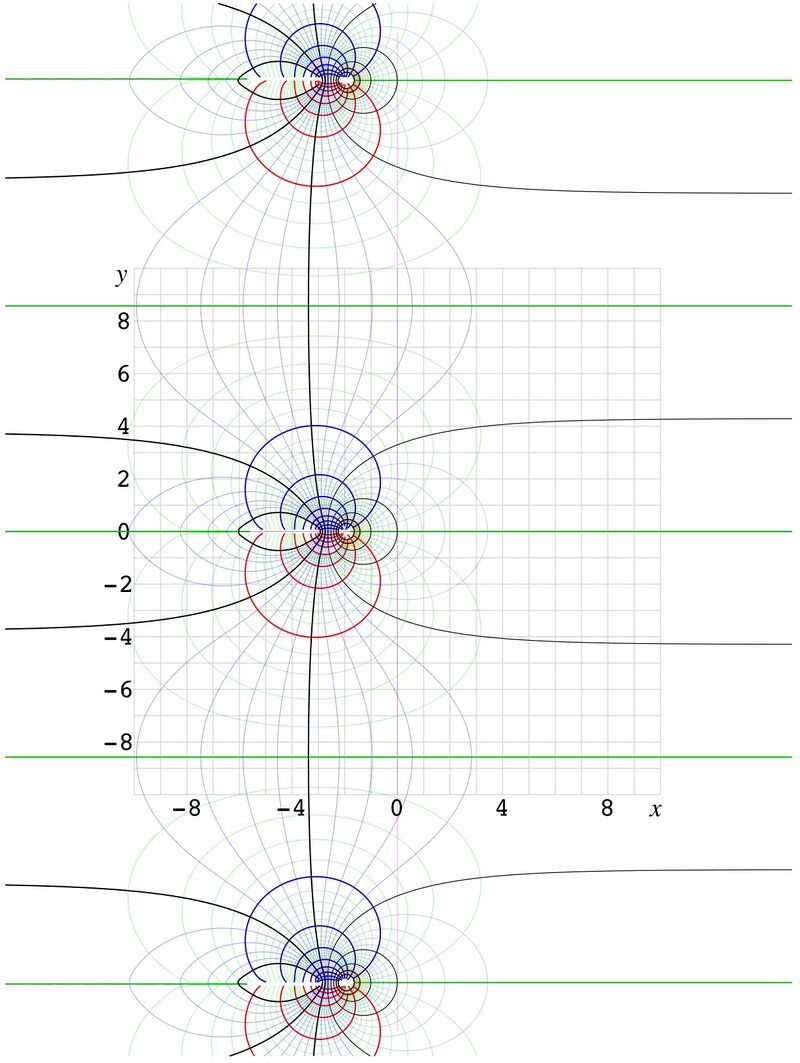
Base 2. Ackermann function

FIg.4. Ackermann function $f=A(4,z)=F_{2}(z+3)-3$ at the complex $z$ plane. Grid covers the range ( $-10\leq \Re (z)\leq 10~,~-4\leq \Im (z)\leq 4$ with unit step. Levels of integer values of the real part and the same for imaginary part are shown with thick lines.

Tertration at base 2 can be expressed through the 4th Ackermann function $F_{2}(z)=A(4,z-3)+3$ This Ackermann function is plotted in fig.4. As base $b>\exp(1/{\rm {e)}}$, the function is not periodic. However, there is asymptotic periods $L$ and $L^{*}$ in the upper and lower half-planes. In vicinity of positive part of the real axis, the function shows rapid growth, and it is not possible to draw the levels there. All the singularities of the Ackermann function are at the negative integer values smaller than $-4$.

Base e. Natural tetration

Fig.5.Analytic tetration at the base e , $f=F_{\rm {e}}(z)$ in the complex $z$plane. The grid covers the range ($-9\leq \Re (z)\leq 9$, $-4\leq \Im (z)\leq 4$). Levels $|f|=\exp(0),\exp(\pm 1),\exp(\pm 2),..$ and levels ${\rm {Arg}}(f)=0,\pm 1,\pm 2,\pm 3$ are shown with thick lines.

Base $b-{\rm {e}}$ is the most natural choise. In this case, the increment $Q$ is equal to the asymtotic value $L$.

At the translation for inity along the real axis,

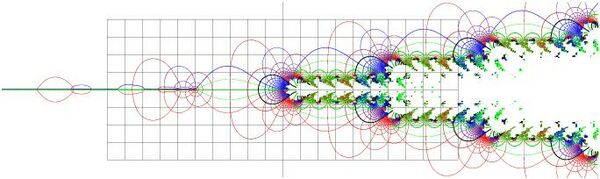
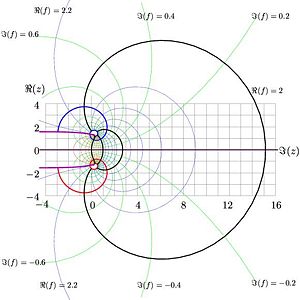
Superlogarithm

Fig.7. Inverse of the analytic tetration $f=F_{\rm {e}}^{-1}(z)$ at the complex $z$-plane.

Inverse of the natural tetration can be considered as superlogarithm. Equilines of funciton $f=F_{\rm {e}}^{-1}(z)$ are shown in Figure 7. Levels of integer real part and those of integer imaginary part are shown with thick lines. This function has two branchpoints at eigenvalues of logarithm. In the figure, the cuts are placed along the lines $\Re (f)=-2$; then, the function is regular in vicinity of the real axis, approaching the limitig value $-2$ at $-\infty$ and slowly growing up at positive values of the argument.

Discussion

Analytic tetrations are shown for base $b={\sqrt {2}}$, $b=2$, and $b={\rm {e}}$. In the similar way, the tetration on other bases (for example, $b=10$ ) can be plotted.

Knowledge of the asymptotic behavior gives the key to the efficient evaluation.

references

See also the discussion at http://math.eretrandre.org/tetrationforum/forumdisplay.php?fid=3