Heat of vaporization

The heat of vaporization, ($H_{v}$ or $H_{vap}$) is the amount of thermal energy required to convert a quantity of liquid into a vapor. It can be thought of as the energy required to break the intermolecular bonds within the liquid.

It is also often referred to as the latent heat of vaporization ($LH_{v}$ or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_v} ) and the enthalpy of vaporization (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta H_v} or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta H_{vap}} or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta_v H} ) and is usually measured and reported at the temperature corresponding to the normal boiling point of the liquid. Sometimes reported values have been corrected to a temperature of 298 K.

Measurement units

Heat of vaporization values are usually reported in measurement units such as J/mol or kJ/mol and referred to as the molar heat of vaporization, although J/g or kJ/kg are also often used. Older units such as kcal/mol, cal/g, Btu/lb and others are still used sometimes.

(GNU) Diagram: Wilfried Cordes
Figure 1: Heats of vaporization versus temperature.

Temperature dependency

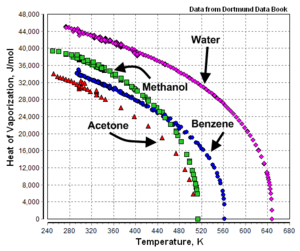
The heat of vaporization is not a constant. It is temperature dependent as shown in Figure 1 by the example graphs of temperature versus heat of vaporization for acetone, benzene, methanol and water.

As shown by the example graphs, the heat of vaporization of a liquid at a given temperature (other than the normal boiling point temperature) may vary significantly from the value reported at the normal boiling point of the liquid.

Estimating heat of vaporization values

Heats of vaporization can be measured calorimetrically and measured values are available from a number of sources. However, data is not always available for certain liquids or at certain temperatures. In such cases, estimation of heats of vaporization can be made by any of a large number of different methods. Four of the commonly used methods are discussed in the following sections.

Using the Clausius-Clapeyron equation

This integrated form of the Clausius-Clapeyron equation can be used to provide a good approximation of the heat of vaporization for many pure liquids:

(1)     Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \log_e \left( \frac{\; p_2}{p_1} \right) = \frac{\;H_v}{R} \left( \frac{1}{T_1} - \frac{1}{T_2} \right)}

which can be re-arranged to obtain:

(2)     Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_v = R\cdot \log_e \left( \frac{\; p_2}{p_1} \right) \left(\frac{\; T_2 \cdot T_1}{T_2 - T_1}\right)}

where:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_v}	= Heat of vaporization, in J/mol
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R}	= 8.3144 = Universal gas constant, in J/(K Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cdot} mol)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle log_e}	= Logarithm on base Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_1}	= The liquid's vapor pressure at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_1} , in atm
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_2}	= The liquid's vapor pressure at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_2} , in atm
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_1}	= Temperature, in K
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_2}	= Temperature, in K

Table 1: Heat of vaporization, normal boiling point and critical temperature and pressure of various liquids Name Formula Hv Tn Tc pc ( J/mol ) ( °C ) ( K ) ( K ) ( atm ) Acetic acid C2H4O2 23,700 117.9 391.1 594.8 57.1 Acetone C3H6O 29,100 56.2 329.4 508.7 47.0 Benzene C6H6 30,720 80.0 353.2 562.1 48.6 Butane C4H10 22,440 – 0.5 272.7 425.2 37.5 Carbon tetrachloride CCl4 29,820 76.6 349.8 556.3 45.0 Chloroform CHCl3 29,240 61.1 334.3 536.2 54.0 Cyclopentane C5H10 27,300 49.2 322.4 511.8 44.6 Ethanol C2H6O 38,560 78.2 351.4 516.2 63.0 Hexane C6H14 28.850 68.7 341.9 507.4 29.9 Methanol CH4O 35,210 64.7 337.9 513.2 78.5 Water H20 40,660 100 373.2 647.3 218.3 Notes: (1) Hv = heat of vaporization at the normal boiling point (2) Tn = normal boiling point (3) Tc = critical temperature (4) pc = absolute critical pressure

The primary Clausius-Clapeyron equation is exact. However, the above integrated form of the equation is not exact because it is necessary to make these assumptions in order to perform the integration:

• The molar volume of the liquid phase is negligible compared to the molar volume of the vapor phase
• The vapor phase behaves like an ideal gas
• The heat of vaporization is constant over the temperature range as defined by T₁ and T₂

As an example of using the Clausius-Clapeyron equation, given that the vapor pressure of benzene is 1 atm at 353 K and 2 atm at 377 K, benzene's heat of vaporization is obtained as 32,390 J/mol within that temperature range.

Using Riedel's equation

Riedel proposed an empirical equation for estimating a liquid's heat of vaporization at its normal boiling point. The equation may be expressed as:

(3)     Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_v = \frac{1.092\, R\, T_n\, (\log_e p_c -\, 1.013)}{0.930 - (T_n/T_c)}}

where:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_v}	= Heat of vaporization, in J/mol
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R}	= 8.3144 = Universal gas constant, in J/(K Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cdot} mol)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_n}	= The liquid's normal boiling point, in K
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c}	= The liquid's critical temperature, in K
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle log_e}	= Logarithm on base Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_c}	= The liquid's critical pressure at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_n} , in bar

For an empirical expression, equation (3) is surprisingly accurate and its error rarely exceeds 5 %. For example, using water data (see Table 1) of T_n = 373.2 K,
T_c = 647.3 K and P_c = 221.2 bar (218.3 atm), the heat of vaporization is obtained as 42,060 J/mol. That is within 3 percent of the 40,660 J/mol in Table 1.

Table 2: Application of Trouton's rule Name Hv Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle/} Tn Acetone 90.6 Benzene 87.3 Butane 82.3 Cyclohexane 84.8 Octane 87.3

Using Trouton's rule

Troutons's rule, dating back to 1883, is a relation between a liquid's heat of vaporization and it's normal boiling point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_n} . It provides a good approximation of the heat of vaporization at the normal boiling point of many pure substances, and it may be expressed as:

(4)     Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{H_v}{T_n} \approx 87\;\, \mathrm{to}\;\, 88}

Table 2 provides some examples of the application of Trouton's rule.

Trouton's rule fails for liquids with boiling points below 150 K. It also fails for water, alcohols, amines and liquid ammonia.

Using Watson's equation

Given the heat of vaporization of a liquid at any temperature, its heat of vaporization at another temperature may be estimated by using the Watson equation:

(5)     Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{H_{v2}}{H_{v1}} = \left[\frac{1 - (T_2/T_c)}{1 - (T_1/T_c)}\right]^{0.38}}

which can be re-arranged to obtain:

(6)     Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{H_{v2}}{H_{v1}} = \left(\frac{T_c - T_2}{T_c - T_1}\right)^{0.38}}

where:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{v1}}	= Heat of vaporization of the liquid at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_1} , in J/mol
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{v2}}	= Heat of vaporization of the liquid at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_2} , in J/mol
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_1}	= Temperature, in K
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_2}	= Temperature, in K
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c}	= Critical temperature of the liquid, in K

Watson's equation has achieved wide acceptance and is simple and reliable.