User:Dmitrii Kouznetsov/Analytic Tetration: Difference between revisions
imported>Dmitrii Kouznetsov |
Pat Palmer (talk | contribs) m (Text replacement - "George Orwell" to "George Orwell") |
||
| (45 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{AccountNotLive}} | |||
{{Image|AnalyticTetrtionBase2figure0.jpg|right|200px|Fig.0. Graphic of analytic tetration <math>f=F_2(x)=\exp_2^x(1)</math> versus <math>x</math>.}} | |||
<!-- | <!-- | ||
{{Image|ExampleEquationLog01.png|right|300px|FIg.1. Example of graphic solution of equation <math>L=\log_b(L)</math> for | |||
<math>b=\sqrt{2}</math> (two real solutions, <math>L=2</math> and <math>L=4</math>), | <math>b=\sqrt{2}</math> (two real solutions, <math>L=2</math> and <math>L=4</math>), | ||
<math>b=\exp(1/\rm e)</math> (one real solution <math>L=\rm e</math>) | <math>b=\exp(1/\rm e)</math> (one real solution <math>L=\rm e</math>) | ||
<math>b=2</math> (no real solutions). | <math>b=2</math> (no real solutions).}}!--> | ||
In this page, I collect pieces and figures, which can be used to build-up [[tetration]]. | |||
==Abstract== | ==Abstract== | ||
| Line 18: | Line 19: | ||
Especially I invite | Especially I invite | ||
*Arthur Knoebel | *Arthur Knoebel | ||
*Henryk | *Henryk Trappmann | ||
*Andrew Robbins | *Andrew Robbins | ||
to edit this file.<!-- (they already have found several misprints in my previous postings.)!--> | to edit this file.<!-- (they already have found several misprints in my previous postings.)!--> | ||
| Line 36: | Line 37: | ||
(1) <math>F_b(z)=\exp_b^z(1)</math> | (1) <math>F_b(z)=\exp_b^z(1)</math> | ||
is combination of <math> | is combination of <math>z</math> exponentials on base <math>b</math>. For example, | ||
: <math>~ F_b(0)=\exp_b^0(1)=1</math> | : <math>~ F_b(0)=\exp_b^0(1)=1</math> | ||
: <math>~ F_b(1)=\exp_b(1)=b</math> | : <math>~ F_b(1)=\exp_b(1)=b</math> | ||
: <math>~ F_b(2)=\exp_b^2(1)=\exp_b(\exp_b(1))=b^b</math> | : <math>~ F_b(2)=\exp_b^2(1)=\exp_b(\exp_b(1))=b^b</math> | ||
: <math>~ F_b(3)=\exp_b^3(1)=\exp_b\Big(\exp_b\big(\exp_b(1)\big)\Big)=b^{b^b}</math> | : <math>~ F_b(3)=\exp_b^3(1)=\exp_b\Big(\exp_b\big(\exp_b(1)\big)\Big)=b^{b^b}</math> | ||
and so on. However, such definition is good only for positive integer values of <math> | and so on. However, such definition is good only for positive integer values of <math>z</math>. In general, the superexponential can be defined through the [[Abel equation]] | ||
(2) <math>~\exp_b\Big(F_b(z)\Big)=F_b(z+1) </math> | (2) <math>~\exp_b\Big(F_b(z)\Big)=F_b(z+1) </math> | ||
with additional condition that | with additional condition that | ||
| Line 50: | Line 51: | ||
In this paper, the way to define tetration for non-integer argument is described. For real values of the argument, at <math>~b=2</math>, such a tetration is plotted on figure 0. In the following sections, | In this paper, the way to define tetration for non-integer argument is described. For real values of the argument, at <math>~b=2</math>, such a tetration is plotted on figure 0. In the following sections, | ||
I describe, why is it so important, how to define the tetration for non-integer values of the argument, how can it be evaluated with high precision and why it is the only correct way to define analytic tetration. | I describe, why is it so important, how to define the tetration for non-integer values of the argument, how can it be evaluated with high precision and why it is the only correct way to define analytic tetration. | ||
===Table of superfunctions=== | |||
There exist many basefuncitons such that the supercunctions can be expressed in the closed form. | |||
For some function <math>F</math> such that both <math>F</math> and <math>F^{-1}</math> | |||
can be expressed with simple and explicit formulas, the basefunciton | |||
:<math>H(z)=F(1+H^{-1}(z))</math>. | |||
In such a way, the table below can be constructed. | |||
===Additional argument=== | ===Additional argument=== | ||
| Line 62: | Line 70: | ||
<math>\exp_b^m(F_b(z))=F_b(z+m)</math> | <math>\exp_b^m(F_b(z))=F_b(z+m)</math> | ||
The generalization to non-integer values of <math>m</math> is possible. | |||
While writing formal expressions (and assuming existence of the inverse function <math>F^{-1}</math>), the | |||
specific preperties of exponential function are not used; and the | |||
generalization is possible. Such generalization is described in article [[User:Dmitrii Kouznetsov/loginal]]. | |||
===Inverse function and group properties=== | ===Inverse function and group properties=== | ||
| Line 68: | Line 81: | ||
and | and | ||
<math>~\exp(z)</math> instead of <math>~\exp_b(z)</math>; | <math>~\exp(z)</math> instead of <math>~\exp_b(z)</math>; | ||
omitting indices. However, you may recover them at any moment. | |||
(I am not sure which notation is best. D.) | (I am not sure which notation is best. D.) | ||
| Line 97: | Line 110: | ||
===Ambiguity of the real-analytic extension=== | ===Ambiguity of the real-analytic extension=== | ||
== | ==[[Abel equation]]== | ||
Assume, the tetration <math>F</math> is defined with the [[Abel equation]] | Assume, the tetration <math>F</math> is defined with the [[Abel equation]] | ||
| Line 105: | Line 118: | ||
(11) <math> F(0)=1</math> | (11) <math> F(0)=1</math> | ||
==Asymptotic== | |||
The analytic extension of tetration <math>~F(z)</math> is supposed to grow | |||
fast along the real axis of the complex <math>z</math>-plane, | |||
at least for some values of base <math>b</math>. | |||
However, it has no need to grow infinitely in the direction of imaginary axis. For mathematics of computation, it would be better, if <math>F(x+{\rm i} y)</math> remains bounded at <math>y\rightarrow +\infty</math>. Consider this possibility. | |||
Assume, there exist solution <math>F(z)</math> of equations | |||
(10), (11), analytic in the <math>\Re(z) \ge 0</math>, with, probably, countable number of cuts and singularities at <math>\Re(z)<0</math>, | |||
with exponential asymptotic behavior | |||
(12) <math> F(z)=L+\varepsilon(z) + o \big(\varepsilon(z)^{2}\big) </math> | |||
within some range,<!-- between cuts, $\Im(z)>0$, !--> | |||
where | |||
(13) <math> \varepsilon(z)=\exp(Qz+r) </math>, | |||
<math>Q</math> and <math>r</math> are fixed complex numbers, | |||
and <math>L</math> is eigenvalue of logarithm, solution of equation | |||
(14) <math> x=\log_{b}(x)</math>. | |||
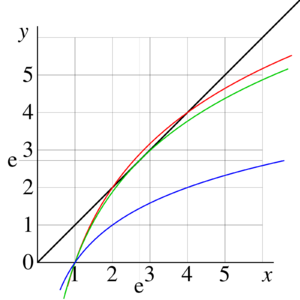
{{Image|ExampleEquationLog01.png|right|300px|FIg.1. Example of graphic solution of equation | |||
<math>x=\log_b(x)</math> for | |||
<math>b=\sqrt{2}</math> (two real solutions, <math>x=2</math> and <math>x=4</math>), | |||
<math>b=\exp(1/\rm e)</math> (one real solution <math>x=\rm e</math>) | |||
<math>b=2</math> (no real solutions).}} | |||
Solutions of equation (14) are called [[fixed point]]s of logarithm. | |||
Three examples of graphical solution of equation (14) are shown in figure 1 for | |||
<math>b=\sqrt{2}</math>, | |||
<math>b=\exp(1/\rm e)</math>, and | |||
<math>b=2</math>. | |||
The black line shows function <math> y=x</math> in the <math>x,y</math> plane. | |||
The colored curves show function <math> y=\log_b(x)</math> for cases | |||
<math>b=\sqrt{2}</math> (red), | |||
<math>b=\exp(1/\rm e)</math> (green), and | |||
<math>b=2</math> (blue). | |||
At | |||
<math>b=\sqrt{2}</math>, there exist 2 solutions, | |||
<math>x=2</math> and | |||
<math>x=4</math>. | |||
At | |||
<math>b=\exp(1/\rm e)</math> there exist one solution | |||
<math>x=\rm e</math>. | |||
and <math>b=2</math>, there are no real solutions.<br> | |||
In general, | |||
*at <math>b<\exp(1/\rm e)</math> there are two real solutions | |||
*at <math>b=\exp(1/\rm e)</math>, there is one soluition, and | |||
*at <math>b>\exp(1/\rm e)</math> there esist two solutions, but they are complex. | |||
In particular, | |||
at | |||
<math> b=\sqrt{2}</math>, the solutions are <br> | |||
<math>x=L_{\sqrt{2},1}=2</math> and | |||
<math>x=L_{\sqrt{2},2}=4 </math> <br>. | |||
At | |||
<math> b=2</math>, the solutions are <br> | |||
<math>x=L_2 \approx 0.824678546142074222314065+1.56743212384964786105857 \!~\rm i </math> and<br> | |||
<math>x=L_2^*\approx 0.824678546142074222314065-1.56743212384964786105857 \!~\rm i </math>. | |||
At <math> b=\rm e</math>, the solutions are<br> | |||
<math>x=L_{\rm e} \approx 0.318131505204764135312654+1.33723570143068940890116 \!~\rm i</math> | |||
and<br> | |||
<math>x=L_{\rm e}^* \approx 0.318131505204764135312654-1.33723570143068940890116 \!~\rm i</math>. | |||
Few hundred straightforward iterations of equation (14) are sufficient to get the error smaller than the last decimal digit in the approximations above. | |||
The solutions | |||
<math>x=L_1 </math> and | |||
<math>x=L_2 </math> of equation (14) are plotted in figure 2 versus | |||
<math>\beta=\ln(b)</math> with thin black lines. Let | |||
<math>L_1<L_2 </math>, and only at | |||
<math>\ln(b)=1/e </math>, the equality | |||
<math>L_1=L_2 </math> takes place. | |||
{{Image|TetrationAsymptoticParameters01.jpg|right|700px|FIg.2. parameters of asymptotic of tetration versus logarithm of the base}} | |||
The thin black solid curve at | |||
<math> \beta \ge 1/\rm e</math> represents the real part of the solutions | |||
<math>L </math> and | |||
<math>L^* </math> of (14); the thin black dashed curve represents the two options for the imaginary part; the two solutions are complex conjugaitons of each other. Let | |||
<math>\Re(L)>0</math>. | |||
===Increment and periodicity=== | |||
Parameter | |||
<math> Q </math> in equaiton (13) has sense of asymptotic increment. Consider possible values of <math>Q</math>. | |||
Substitution of expression (13) into the eq. (12) gives<br> | |||
<math> L+\varepsilon(z) {\rm e}^Q+o(\varepsilon(z))=\exp\!\Big(\ln(b)(L+\varepsilon(z)+o(\varepsilon(z))\Big) </math> | |||
Using equation (14) gives<br> | |||
<math> L+\varepsilon(z){\rm e}^Q+o(\varepsilon(z)) = L~\Big(1+ \ln(b)\varepsilon(z) +o(\varepsilon(z))\Big) </math> | |||
Then | |||
(16) <math> Q=\ln(\ln(b))+\ln(L) </math>. | |||
At | |||
<math>\ln(b)<1/\rm e </math>, the two real increments correspond the the two real eigenvalues of logarithm. Let | |||
<math> Q_1=\ln(\ln(b))+\ln(L_1) </math> and | |||
<math> Q_2=\ln(\ln(b))+\ln(L_2) </math>. | |||
Both | |||
<math> Q_1 </math> and <math> Q_2 </math> are plotted in Figure 2 with thick solid lines; | |||
<math> Q_1\le 0 </math> and <math> Q_2\ge 0 </math>, and only at | |||
<math>\ln(b)=1/\rm e </math> the equality | |||
<math> Q_1= Q_2= 0 </math> holds. | |||
In such a way, at <math>\ln(b)<1/\rm e</math>, there exist positive increment, which corresponds to <math>L_2</math> and means, that the perturbation <math>\epsilon(z)</math> of the stationary solution grows up in the diredtion of real axis; there exist negative increment (decrement, if you like), which corresponds to <math>L_1</math> and indicates, that the perturbation grows up in the opposite direction. | |||
At <math>0<\ln(b)<2/\rm e</math>, there may exist tetration <math> F(z)</math> with two different asumptotics. | |||
At large positive values of <math>\Re(z)</math> it decays to the <math>L_1</math> and | |||
At large negative values of <math>\Re(z)</math> it decays to the <math>L_2</math>. | |||
At | |||
<math>\ln(b)\ge 1/\rm e </math>, there exist two possible increments, | |||
<math>Q</math> and <math>Q^*</math>. The real part of <math>Q</math> is plotted with thick solid line, and the imaginary part is shown with thick dashed line. The real part is positive; id est, the perturbation | |||
<math>\varepsilon(z)</math> grows up in the direction of real axis. | |||
For computational mathematics, it would be good ot construct the solution, that decays both in the direction of the imaginary asis and in the opposite direction. Such a solution should have asymptotics (12),(13) at large positive values of the imaginary part of the argument and its conjugation at large negative imaginary part of the argument. | |||
The exponential asymptotics implies the asumptotic perioditity. The period | |||
<math>T=\frac{2 \pi{\rm i}}{Q} </math> | |||
is shown in FIgure 2 with dotted lines; for the case when period is negative, the minus period is plotted. It is amaising, that at <math>\ln(b)>1/\rm e</math>, the imajinary part is slightly larger than unity and remains almost constant. | |||
In particular, at <math>b=\sqrt{2}</math>, the periods are | |||
<math> T_{\rm b,1} = \frac{2\pi \rm i}{Q_{b,1}}\approx -17.143148179354847104 \!~\rm i | |||
</math><br> | |||
<math> T_{\rm b,2} = \frac{2\pi \rm i}{Q_{b,2}}\approx ~ 19.236149042042854710 \!~\rm i | |||
</math><br> | |||
At | |||
<math> b=2</math>, the asymptotic period<br> | |||
<math> T= 5.58414243554338946020010 + 1.05421836033693734654000\!~ \rm i</math>; | |||
<br> | |||
and at | |||
<math>b=\rm e</math>, the asymptotic period<br> | |||
<math> T= 4.44695072006700782711227 + 1.05793999115693918376341 \!~ \rm i</math>. | |||
While one deal with real axis, one imagine some real-analytic extension shown in Figure 0 and consider also | ===Uniqueness=== | ||
While one deal with solutions of system (10), (11) at the real axis, one imagine some real-analytic extension shown in Figure 0 and consider also | |||
( | (100) <math> G(z)=F(z+k(z))</math> | ||
where | where | ||
( | (101) <math> k(z)=\sum_{n=-\infty}^{\infty} \alpha_n \exp(2\pi {\rm i} n z)</math> | ||
Such a funciton is also | Such a funciton is also soluiton of the Abel equation; at | ||
( | (102) <math> \alpha_{-n}=(\alpha_n)^* </math> | ||
and | and | ||
( | (103) <math> \alpha_0=-\sum_{n\ne 0} \alpha_n</math> | ||
function <math>~G</math> is real and passes through the same points as </math>~F</math> at integer values of the argument. | function <math>~G</math> is real and passes through the same points as </math>~F</math> at integer values of the argument. | ||
| Line 130: | Line 280: | ||
However, the difference between functions | However, the difference between functions | ||
<math>~F</math> and | <math>~F</math> and | ||
<math>~G</math> | <math>~G</math> becomes seen, if one of them, for example, <math>~F</math>, is analytic and regular in some wide range, function <math>~G(z)</math> will be analytic only within the strip <math>~|z|<y_0</math>; order of magnitude of | ||
function <math>~G(z)</math> will be analytic only within the strip <math>~|z|<y_0</math>; order of magnitude of | |||
<math>~y_0</math> can be estimated with | <math>~y_0</math> can be estimated with | ||
<math>y_0 \approx {\rm MIN}_n ~ \frac{ \ln(2/|\alpha_n|)}{2\pi n}</math> | <math>y_0 \approx {\rm MIN}_n ~ \frac{ \ln(2/|\alpha_n|)}{2\pi n}</math> | ||
At larger values of the imaginary part of the | At larger values of the imaginary part of the argument, the periodic function <math>k</math> takes huge values, including various negative integers. Namely at these values, function <math>~F</math> has singulatities. | ||
Various functions may satisfy equations (2),(3). | |||
For an abstract excersise in comlex functional analysis, [[all animals are created equal]]. However, for the applicaitons in the computational mathematics, [[some of them are more equal than other]] | |||
<ref name="orwell">'''All animals are created equal''' and that with addition '''BUT SOME ANIMALS ARE MORE EQUAL THAN OTHERS''' are slogans of animals in the novel [[Animal farm]] by George Orwell. (Animals gained the superior power at the farm, bushing out the farmer). First slogan was used to gain the power. The second part appeared when pigs begun to justify their privilegies.</ref>. | |||
As such a ''more equal animal'' we should choose the solution with simplest behavior, with minimum of singulatities, and easiest for the evaluation. | |||
<!-- | <!-- | ||
==Exponential asymptotic== | ==Exponential asymptotic== | ||
Consider tetration with following asymptotic behavior: | Consider tetration with following asymptotic behavior: | ||
| Line 186: | Line 305: | ||
Quasi-period <math>T=2\pi/Q</math> is plotted with dotted lines. | Quasi-period <math>T=2\pi/Q</math> is plotted with dotted lines. | ||
!--> | |||
At small base, both values of quasiperiod are pure imaginary. This periodic or quasi-periodic behavior is similar to that of the conventional exponential, | At small base, both values of quasiperiod are pure imaginary. This periodic or quasi-periodic behavior is similar to that of the conventional exponential, | ||
| Line 193: | Line 313: | ||
At <math>~b> \exp(1/{\rm e})</math> values of period <math>T</math> are complex; and | At <math>~b> \exp(1/{\rm e})</math> values of period <math>T</math> are complex; and | ||
<math>\Re(T)>0</math>. This corresponds to the exponential growth of the asymptotic solution in the direction of the real axis; at large positive values of <math>\Re(Qz)</math> the asymptotic does not approximate the function which grows faster than any exponential. | <math>\Re(T)>0</math>. This corresponds to the exponential growth of the asymptotic solution in the direction of the real axis; at large positive values of <math>\Re(Qz)</math> the asymptotic does not approximate the function which grows faster than any exponential. | ||
==Examples of tetration at different bases== | |||
===Small base. Base <math>b=\sqrt{2}</math>=== | ===Small base. Base <math>b=\sqrt{2}</math>=== | ||
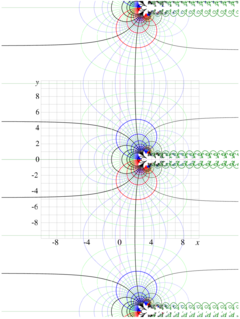
{{Image|AnalyticTetrationBaseSqrt2v00.jpg|right|220px|Fig.3a. Tetration <math>f=F(z)</math> at the complex <math>z</math>-plane. | |||
Levels of integer <math>\Re(f)</math> and levels of integer <math>\Im(f)</math> are shown with thick lines. | Levels of integer <math>\Re(f)</math> and levels of integer <math>\Im(f)</math> are shown with thick lines. | ||
Grid covers with unit step range | <!--Grid covers with unit step range | ||
(<math>-10\le \Re(z) \le 10 </math>, | (<math>-10\le \Re(z) \le 10 </math>, | ||
<math>-10\le \Im(z) \le 10 </math>). | <math>-10\le \Im(z) \le 10 </math>).!-->}} | ||
For evaluation of Tetration we need to assume that it exists, and has asymptotic (30). | For evaluation of Tetration we need to assume that it exists, and has asymptotic (30). | ||
| Line 206: | Line 328: | ||
the function has periodic behavior in the direction of imaginary axis, as it is shown in Fig. 3. In this figure, the example with <math>b=\sqrt{2}</math> is used. Function is periodic; period <math>T\approx 17.1431~\rm i</math>. | the function has periodic behavior in the direction of imaginary axis, as it is shown in Fig. 3. In this figure, the example with <math>b=\sqrt{2}</math> is used. Function is periodic; period <math>T\approx 17.1431~\rm i</math>. | ||
The limiting values: | |||
<math> \lim_{x \rightarrow \infty} F_\sqrt{2}(x+{\rm i}y)=2</math> | |||
<math> \lim_{x \rightarrow -\infty} F_\sqrt{2}(x+{\rm i}y)=4</math> | |||
At non-zero values of the imaginary part of the argument, the function decays | At non-zero values of the imaginary part of the argument, the function decays | ||
| Line 223: | Line 345: | ||
As all other tetrations, it has singularity at <math>z=-2</math>, | As all other tetrations, it has singularity at <math>z=-2</math>, | ||
<math>~F(-1)=0</math> and <math>~F(0)=1</math>. | <math>~F(-1)=0</math> and <math>~F(0)=1</math>. | ||
===Base <math>b=\sqrt{2}</math>, alternative tetration <math>G</math>=== | |||
{{Image|AnalyticTetrationBaseSqrt2u00.png|left|240px|Fig.3b. Tetration <math>f=G(z)</math> at the complex plane <math>z=x+{\rm i}y</math>. | |||
Levels of integer <math>\Re(f)</math> and levels of integer <math>\Im(f)</math> are shown with thick lines. | |||
<!--Grid covers with unit step range | |||
(<math>-10\le \Re(z) \le 10 </math>, | |||
<math>-10\le \Im(z) \le 10 </math>).!-->}} | |||
Along the real axis, such a solution grows up faster than any exponential; it is always larger than 4 and therefore cannot be equal to unity; so, it is not possible to satisfy condition <math>G(0)=0</math> just shifting its argument for some constant. The behavior of tetration <math>G_{\sqrt{2}}</math> along the real axis makes it similar to that of tetrations with <math>b > \exp(1/\rm e)</math>; although, the larger | |||
<math>b</math>, the larger is the growth. | |||
===More alternative tetrations=== | |||
Alternative tetration <math> G </math> as solution of equation (1) can be calculated if we withdraw condition (2), and substitute it to | |||
<math> | |||
G(z)=L_{b,2}+\exp(Q_2 z)+o( \exp(Q_2 z)) | |||
</math> | |||
Such a solution is shown in Figure 3b. | |||
Other, more singular tetrations can be obtained by light periodic deformation of the argument. | Other, more singular tetrations can be obtained by light periodic deformation of the argument. | ||
=== Base 2. Ackermann function=== | === Base 2. Ackermann function=== | ||
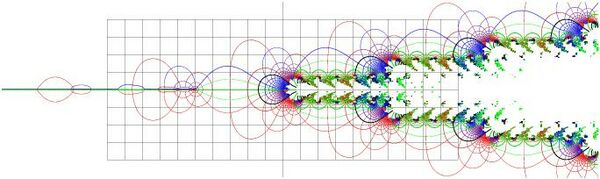
{{Image|Analytic4thAckermannFunction00.jpg|right|600px| FIg.4. | |||
Ackermann function <math>f=A(4,z)=F_2(z+3)-3</math> at the complex <math>z</math> plane. | Ackermann function <math>f=A(4,z)=F_2(z+3)-3</math> at the complex <math>z</math> plane. | ||
Grid covers the range ( | Grid covers the range ( | ||
| Line 233: | Line 372: | ||
-10 \le \Re(z) \le 10 ~,~ | -10 \le \Re(z) \le 10 ~,~ | ||
-4 \le \Im(z) \le 4 </math> with unit step. | -4 \le \Im(z) \le 4 </math> with unit step. | ||
Levels of integer values of the real part and the same for imaginary part are shown with thick lines. | Levels of integer values of the real part and the same for imaginary part are shown with thick lines.}} | ||
Tertration at base 2 can be expressed through the 4th [[Ackermann function]] | Tertration at base 2 can be expressed through the 4th [[Ackermann function]] | ||
<math>F_2(z)=A(4,z-3)+3</math> | <math>F_2(z)=A(4,z-3)+3</math> | ||
This Ackermann function is plotted in fig.4. As base | This Ackermann function is plotted in fig.4. As base | ||
<math>b > \exp(1/\rm e)</math>, the function is not periodic. However, there | <math>b > \exp(1/\rm e)</math>, the function is not periodic. However, there are asymptotic periods | ||
<math>L</math> and <math>L^*</math> | <math>L</math> and <math>L^*</math> | ||
in the upper and lower half-planes. In vicinity of positive part of the real axis, the function shows rapid growth, and it is not possible to draw the levels there. All the singularities are at the negative integer values smaller than - | in the upper and lower half-planes. In vicinity of positive part of the real axis, the function shows rapid growth, and it is not possible to draw the levels there. All the singularities of the Ackermann function are at the negative integer values smaller than <math>-4</math>. | ||
=== Base e. Natural tetration === | === Base e. Natural tetration === | ||
| Line 256: | Line 395: | ||
Base <math>b-\rm e</math> is the most natural choise. In this case, the | Base <math>b-\rm e</math> is the most natural choise. In this case, the | ||
increment <math>Q</math> is equal to the asymtotic value <math>L</math>. | increment <math>Q</math> is equal to the asymtotic value <math>L</math>. | ||
At the translation for inity along the real axis, | At the translation for inity along the real axis, | ||
===Superlogarithm=== | ===Base e. Superlogarithm=== | ||
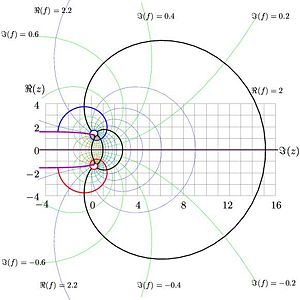
{{Image|Slogez01.jpg|left|300px|Fig.7. Inverse of the analytic tetration | |||
<math>f=F_{\rm e}^{-1}(z)</math> at the complex <math>z</math>-plane. | <math>f=F_{\rm e}^{-1}(z)</math> at the complex <math>z</math>-plane.}} | ||
Inverse of the natural tetration can be considered as superlogarithm. | Inverse of the natural tetration can be considered as superlogarithm. | ||
| Line 284: | Line 421: | ||
<references/> | <references/> | ||
See also the discussion at http://math.eretrandre.org/tetrationforum/forumdisplay.php?fid=3 | See also the discussion at http://math.eretrandre.org/tetrationforum/forumdisplay.php?fid=3 | ||
===Table of superfunctions=== | |||
There exist many basefuncitons such that the supercunctions can be expressed in the closed form. | |||
[[ | For some function <math>F</math> such that both <math>F</math> and <math>F^{-1}</math> | ||
can be expressed with simple and explicit formulas, the basefunciton | |||
:<math>H(z)=F(1+F^{-1}(z))</math>. | |||
In such a way, the table below can be constructed. | |||
{|class="wikitable" | |||
! <math>H(z)</math> | |||
! <math>F(z)</math> | |||
! <math>F^{-1}(z)</math> | |||
! comment | |||
|- | |||
|<math>z+\!\!+</math>||<math>b+z</math>||<math>z-b</math> || | |||
|- | |||
|<math>z+b</math>||<math>bz+c</math> || <math>(z-c)/b</math> || | |||
|- | |||
|<math>cz+c</math>||<math>(b^z+\frac{c}{1-b})d</math>||<math>\log_b\frac{z-\frac{cd}{1-b}}{d}</math>|| | |||
|- | |||
|<math>b^z</math> || <math>\mathrm{tet}_b(z)</math> || <math>\mathrm{arctet}_b(z)</math>||[[tetration]] | |||
|- | |||
|<math>z^b</math>|| <math>\exp(b^z)</math> || <math>\log_b(\ln(z))</math>|| | |||
|- | |||
|<math>\big(a^b+z^b\big)^{1/b}</math>||<math>az^{1/b}</math>||<math>(z/a)^b</math>|| | |||
|- | |||
|<math>\ln(a+\mathrm{e}^z)</math>||<math>\ln(az)</math>||<math>\exp(z)/a</math>|| | |||
|- | |||
|<math>az/(z+a)</math>||<math>a/z</math>||<math>a/z</math>||amaising, <math>F=F^{-1}</math> | |||
|- | |||
|<math>2z^2-1</math>||<math>\cos(\pi 2^z)</math>||<math>\log_2(\arccos(z)/\pi)</math>|| | |||
|- | |||
|<math>H(z)</math>||<math>F(z)</math>||<math>F^{-1}(z)</math>|| | |||
|- | |||
|<math>P(H(Q(z)))</math>||<math>P(F(z))</math>||<math>F^{-1}(Q(z))</math>|| P(Q(z))=z | |||
|-|} | |||
Latest revision as of 09:20, 14 June 2024
The account of this former contributor was not re-activated after the server upgrade of March 2022.
In this page, I collect pieces and figures, which can be used to build-up tetration.
Abstract
Analytic tetration is defined as mathematical function that coincides witht the tetration at integer values of the argument and is analytic outside the negative part of the real axis. Existence of such a function is postulated; and arguments in favor of uniqueness of such a function are considered. The algorithm of evaluation is suggested. Examples of evaluation, pictures and tables are supplied. The application and the generalization is discussed.
Preface
The colleagues indicated so many misprints in my papers about tetration, posted at my homepage [1], that I want to give them opportunity to correct them in real time.
Especially I invite
- Arthur Knoebel
- Henryk Trappmann
- Andrew Robbins
to edit this file.
I consider the topic very important and urgent. The analytic tetration should be investigated and discussed right now; overvice, the non-analytic extension may become an ugly standard in mathematics of computation; the implementation of hige numbers with non-analytic tetration would make difficult realization of arithmetic operations and cause a lot of incompatibilities.
This is my apology for posting this research now, while the rigorous proof of existence and uniqueness of the analytic tetration is not yet found. My believe is based on the numerical check of the hypothesis of the existence and uniqueness, on smallness of the residual at the substitution of the function to the tetration equation and beauty of the resulting pictures. I cannot imagine that the agreement with 14 decimal digits occurs just by occasion without deep mathematical meaning.
In such a way I apologize for postulating of statements which should be prooven by the rigorous mathematical deduction.
Introduction
Quick start
Roughly, super-exponential
(1)
is combination of exponentials on base . For example,
and so on. However, such definition is good only for positive integer values of . In general, the superexponential can be defined through the Abel equation
(2)
with additional condition that
(3)
Then, at least for positive values of and positive integer values of , such a definition can be used for the evaluation of tetration.
In this paper, the way to define tetration for non-integer argument is described. For real values of the argument, at , such a tetration is plotted on figure 0. In the following sections, I describe, why is it so important, how to define the tetration for non-integer values of the argument, how can it be evaluated with high precision and why it is the only correct way to define analytic tetration.
Table of superfunctions
There exist many basefuncitons such that the supercunctions can be expressed in the closed form. For some function such that both and can be expressed with simple and explicit formulas, the basefunciton
- .
In such a way, the table below can be constructed.
Additional argument
One can consider to add the additional argument, replacing to . This may have sense, while is allowed to have only integer values. However, at the implementation of "good" tetration, the "argument" can be considered as inverse superexponential of some argument, ; then, ; in the way, similar to that of convential logarithms: it is sufficient to investigate properties of natural logarithm ln; then, any other can be expressed as .
The exponentiation of tetration is equivalent to increment of its argument. While summaton operation forms the group, exponentiation does too.
The generalization to non-integer values of is possible. While writing formal expressions (and assuming existence of the inverse function ), the specific preperties of exponential function are not used; and the generalization is possible. Such generalization is described in article User:Dmitrii Kouznetsov/loginal.
Inverse function and group properties
In this section, I write instead of and instead of ; omitting indices. However, you may recover them at any moment.
(I am not sure which notation is best. D.)
The speculation of the previous subseciton can be written shorter.
Assume there exist function such that .
Let and .
Then .
You can put subscript to and in the defuction above, and it will be seen, that we have no need to deal with funciton of 2 variables, considering ; it can be expressed in terms of . However, we need to specify, what set shold be and from in the deduction above: must they be positive integer, or they can be real, of they can be also complex numbers.
History of tetration and huge numbers
Perhaps, every researcher used to see diagnostivs "floating overflow" at the evlauation of an expression with huge numbers....
Ackermann functions
Ambiguity of the real-analytic extension
Abel equation
Assume, the tetration is defined with the Abel equation
(10)
and assume the condition
(11)
Asymptotic
The analytic extension of tetration is supposed to grow fast along the real axis of the complex -plane, at least for some values of base . However, it has no need to grow infinitely in the direction of imaginary axis. For mathematics of computation, it would be better, if remains bounded at . Consider this possibility.
Assume, there exist solution of equations (10), (11), analytic in the , with, probably, countable number of cuts and singularities at , with exponential asymptotic behavior
(12)
within some range, where
(13) ,
and are fixed complex numbers, and is eigenvalue of logarithm, solution of equation
(14) .
Solutions of equation (14) are called fixed points of logarithm. Three examples of graphical solution of equation (14) are shown in figure 1 for , , and .
The black line shows function in the plane. The colored curves show function for cases (red), (green), and (blue).
At , there exist 2 solutions, and .
At there exist one solution .
and , there are no real solutions.
In general,
- at there are two real solutions
- at , there is one soluition, and
- at there esist two solutions, but they are complex.
In particular,
at
, the solutions are
and
.
At
, the solutions are
and
.
At , the solutions are
and
.
Few hundred straightforward iterations of equation (14) are sufficient to get the error smaller than the last decimal digit in the approximations above.
The solutions and of equation (14) are plotted in figure 2 versus with thin black lines. Let , and only at , the equality takes place.
The thin black solid curve at represents the real part of the solutions and of (14); the thin black dashed curve represents the two options for the imaginary part; the two solutions are complex conjugaitons of each other. Let .
Increment and periodicity
Parameter in equaiton (13) has sense of asymptotic increment. Consider possible values of .
Substitution of expression (13) into the eq. (12) gives
Using equation (14) gives
Then
(16) .
At , the two real increments correspond the the two real eigenvalues of logarithm. Let and . Both and are plotted in Figure 2 with thick solid lines; and , and only at the equality holds.
In such a way, at , there exist positive increment, which corresponds to and means, that the perturbation of the stationary solution grows up in the diredtion of real axis; there exist negative increment (decrement, if you like), which corresponds to and indicates, that the perturbation grows up in the opposite direction. At , there may exist tetration with two different asumptotics. At large positive values of it decays to the and At large negative values of it decays to the .
At , there exist two possible increments, and . The real part of is plotted with thick solid line, and the imaginary part is shown with thick dashed line. The real part is positive; id est, the perturbation grows up in the direction of real axis.
For computational mathematics, it would be good ot construct the solution, that decays both in the direction of the imaginary asis and in the opposite direction. Such a solution should have asymptotics (12),(13) at large positive values of the imaginary part of the argument and its conjugation at large negative imaginary part of the argument.
The exponential asymptotics implies the asumptotic perioditity. The period
is shown in FIgure 2 with dotted lines; for the case when period is negative, the minus period is plotted. It is amaising, that at , the imajinary part is slightly larger than unity and remains almost constant.
In particular, at , the periods are
At
, the asymptotic period
;
and at
, the asymptotic period
.
Uniqueness
While one deal with solutions of system (10), (11) at the real axis, one imagine some real-analytic extension shown in Figure 0 and consider also
(100)
where
(101)
Such a funciton is also soluiton of the Abel equation; at
(102)
and
(103)
function is real and passes through the same points as </math>~F</math> at integer values of the argument.
and at small values of coefficients , function looks smooth, and it is difficult to guess, which of them is "true". For this reason, for the standard mathematical representation, the non-analytic stepwice funciton uxp was suggested [2].
However, the difference between functions and becomes seen, if one of them, for example, , is analytic and regular in some wide range, function will be analytic only within the strip ; order of magnitude of can be estimated with
At larger values of the imaginary part of the argument, the periodic function takes huge values, including various negative integers. Namely at these values, function has singulatities.
Various functions may satisfy equations (2),(3). For an abstract excersise in comlex functional analysis, all animals are created equal. However, for the applicaitons in the computational mathematics, some of them are more equal than other [3]. As such a more equal animal we should choose the solution with simplest behavior, with minimum of singulatities, and easiest for the evaluation.
At small base, both values of quasiperiod are pure imaginary. This periodic or quasi-periodic behavior is similar to that of the conventional exponential,
but function does not grow to infinity in the direction of the real axis, aproaching eigenvalue of logarithm.
One example of such a behavior is shown in Figure 3 for . The following section describes, how it was ploted.
At values of period are complex; and . This corresponds to the exponential growth of the asymptotic solution in the direction of the real axis; at large positive values of the asymptotic does not approximate the function which grows faster than any exponential.
Examples of tetration at different bases
Small base. Base
For evaluation of Tetration we need to assume that it exists, and has asymptotic (30).
Consider the case of . at fixed values of real part of the argument, the function has periodic behavior in the direction of imaginary axis, as it is shown in Fig. 3. In this figure, the example with is used. Function is periodic; period .
The limiting values:
At non-zero values of the imaginary part of the argument, the function decays to these asymptotiv values.
At the real axis, the has cut at .
Due to the periodicity, the function has cuts also at
for integer .
As all other tetrations, it has singularity at , and .
Base , alternative tetration
Along the real axis, such a solution grows up faster than any exponential; it is always larger than 4 and therefore cannot be equal to unity; so, it is not possible to satisfy condition just shifting its argument for some constant. The behavior of tetration along the real axis makes it similar to that of tetrations with ; although, the larger , the larger is the growth.
More alternative tetrations
Alternative tetration as solution of equation (1) can be calculated if we withdraw condition (2), and substitute it to Such a solution is shown in Figure 3b.
Other, more singular tetrations can be obtained by light periodic deformation of the argument.
Base 2. Ackermann function
Tertration at base 2 can be expressed through the 4th Ackermann function This Ackermann function is plotted in fig.4. As base , the function is not periodic. However, there are asymptotic periods and in the upper and lower half-planes. In vicinity of positive part of the real axis, the function shows rapid growth, and it is not possible to draw the levels there. All the singularities of the Ackermann function are at the negative integer values smaller than .
Base e. Natural tetration
Base is the most natural choise. In this case, the increment is equal to the asymtotic value .
At the translation for inity along the real axis,
Base e. Superlogarithm
Inverse of the natural tetration can be considered as superlogarithm. Equilines of funciton are shown in Figure 7. Levels of integer real part and those of integer imaginary part are shown with thick lines. This function has two branchpoints at eigenvalues of logarithm. In the figure, the cuts are placed along the lines ; then, the function is regular in vicinity of the real axis, approaching the limitig value at and slowly growing up at positive values of the argument.
Discussion
Analytic tetrations are shown for base , , and . In the similar way, the tetration on other bases (for example, ) can be plotted.
Knowledge of the asymptotic behavior gives the key to the efficient evaluation.
Conclusions
references
- ↑ Publications (Those about tetrations are at the top) http://www.ils.uec.ac.jp/~dima/PAPERS
- ↑ Hoos
- ↑ All animals are created equal and that with addition BUT SOME ANIMALS ARE MORE EQUAL THAN OTHERS are slogans of animals in the novel Animal farm by George Orwell. (Animals gained the superior power at the farm, bushing out the farmer). First slogan was used to gain the power. The second part appeared when pigs begun to justify their privilegies.
See also the discussion at http://math.eretrandre.org/tetrationforum/forumdisplay.php?fid=3
Table of superfunctions
There exist many basefuncitons such that the supercunctions can be expressed in the closed form. For some function such that both and can be expressed with simple and explicit formulas, the basefunciton
- .
In such a way, the table below can be constructed.
| comment | |||
|---|---|---|---|
| tetration | |||
| amaising, | |||
| P(Q(z))=z |