Lemniscate: Difference between revisions
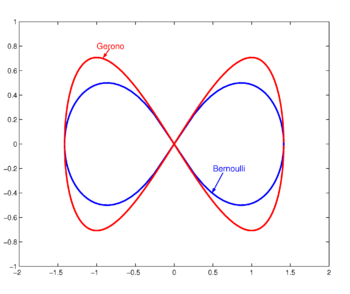
imported>Paul Wormer (New page: {{subpages}} {{Image|Lemniscate.png|right|350px|Blue: lemniscate of Bernoulli (''a''<nowiki>=</nowiki>1); red: lemniscate of Gerono (''a''<sup>2</sup><nowiki>=</nowiki>2)}}. A '''lemniscat...) |
imported>Paul Wormer |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 11: | Line 11: | ||
The figure shows the case ''a'' = √2 | The figure shows the case ''a'' = √2 | ||
==Lemniscate of Bernoulli== | ==Lemniscate of Bernoulli== | ||
This form | This form was discovered by [[Jakob Bernoulli|James Bernoulli]], who coined the term ''Curva Lemniscata'', comparing the curve to a ''noeud de ruban'' (a ribbon knot) in an article in ''Acta Eruditorum'' of September 1694 (p. 336). Basically, Bernoulli's lemniscate is the locus of points that have a distance ''r''<sub>1</sub> to a focus ''F''<sub>1</sub> and a distance ''r''<sub>2</sub> to a focus ''F''<sub>2</sub>, while the product ''r''<sub>1</sub>×''r''<sub>2</sub> is constant. In the figure the foci are on the ''x''-axis at ±1. The product of the distances is constant and equal to half the distance 2''a'' between the foci squared. For foci on the ''x''-axis at ±''a'' the equation is, | ||
:<math> | :<math> | ||
r_1\,r_2 = a^2 = \left[ | r_1\,r_2 = a^2 = \left[ (x-a)^2 + y^2\right]^{\frac{1}{2}} \left[(x+a)^2 + y^2\right]^{\frac{1}{2}}. | ||
</math> | </math> | ||
Expanding and | Expanding and simplifying gives | ||
:<math> | :<math> | ||
(x^2 + y^2)^2 = 2a^2 (x^2 - y^2).\; | (x^2 + y^2)^2 = 2a^2 (x^2 - y^2).\; | ||
| Line 27: | Line 27: | ||
r^4 = 2 a^2 r^2 (\cos^2\theta - \sin^2\theta) \Longrightarrow r^2 = 2 a^2 \cos2\theta. | r^4 = 2 a^2 r^2 (\cos^2\theta - \sin^2\theta) \Longrightarrow r^2 = 2 a^2 \cos2\theta. | ||
</math> | </math> | ||
Bernoulli's lemniscate belongs to the more general class of the [[Cassini ovals]]. | |||
Latest revision as of 10:44, 28 December 2009
.
A lemniscate is a geometric curve in the form of the digit 8, usually drawn such that the digit is lying on its side, as the infinity symbol . The name derives from the Greek λημνισκος (lemniskos, woolen band).
Two forms are common.
Lemniscate of Gerono
This form is named for the French mathematician Camille Christophe Gerono (1799-1891). Its equation in Cartesian coordinates is
- .
The figure shows the case a = √2
Lemniscate of Bernoulli
This form was discovered by James Bernoulli, who coined the term Curva Lemniscata, comparing the curve to a noeud de ruban (a ribbon knot) in an article in Acta Eruditorum of September 1694 (p. 336). Basically, Bernoulli's lemniscate is the locus of points that have a distance r1 to a focus F1 and a distance r2 to a focus F2, while the product r1×r2 is constant. In the figure the foci are on the x-axis at ±1. The product of the distances is constant and equal to half the distance 2a between the foci squared. For foci on the x-axis at ±a the equation is,
Expanding and simplifying gives
The latter equation gives upon substitution of
the following polar equation
Bernoulli's lemniscate belongs to the more general class of the Cassini ovals.


![{\displaystyle r_{1}\,r_{2}=a^{2}=\left[(x-a)^{2}+y^{2}\right]^{\frac {1}{2}}\left[(x+a)^{2}+y^{2}\right]^{\frac {1}{2}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27ecd4b1bdfe764bdc9346e4897032e362f31727)


