Chemical bond: Difference between revisions
imported>Paul Wormer No edit summary |
mNo edit summary |
||
| (41 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{subpages}} | {{subpages}} | ||
{{TOC|right}} | |||
''For further discussion, see also'' [[Theoretical chemistry]] and [[Quantum chemistry]]. | |||
In [[chemistry]], a '''chemical bond''' is an arrangement of [[electron]]s among [[atom]]s that keeps the atoms together. The bond originates in the electrical attraction of opposite charges, and is made possible by the attraction of the positive nucleii of atoms to the electrons associated with them. The central issue in understanding the bond is finding how the electrons associated with atoms distribute their negative charge so as to overcome the natural repulsion between positive atomic cores. A useful understanding can range from an entirely qualitative model based upon the attraction of one atom for electrons compared to another (their [[electronegativity]]) to very detailed computer calculations based upon [[quantum mechanics]]. | |||
It took several centuries before chemical bonding was fully understood, but at present it is generally accepted that non-relativistic quantum mechanical explanations based on Coulomb's electrostatic law<ref>That is, explanations derived from quantum mechanical energy operators containing electron-electron, electron-nucleus, and nucleus-nucleus Coulomb interactions plus electronic kinetic energies.</ref> give satisfactory accounts of all kinds of bonds.<ref>As late as 1916 the famous American chemist [[Gilbert N. Lewis]] disagreed strongly with this statement. He saw electrons as stationary without kinetic energy and not exerting Coulomb forces. In a lecture given at the December meeting of the Sections of Physics and Chemistry of the [[American Association for the Advancement of Science]], the [[American Physical Society]], and the [[American Chemical Society]] (see Science Magazine pp. 297-302 (1917); [http://dx.doi.org/10.1126/science.46.1187.297 DOI]), he declared the following: "Therefore, unless we are willing, under the onslaught of quantum theories, to throw overboard all of the basic principles of physical science, we must conclude that the electron in the Bohr atom not only ceases to obey Coulomb's law, but exerts no influence whatsoever upon another charged particle at any distance." </ref> | If the total energy of two or more bound atoms is lower than the sum of the energies of the free component atoms, the aggregate of atoms form a stable molecule (or crystal) and the energy lowering is the ''binding energy'' of the molecule (or crystal). | ||
The chemical bond takes on many forms, ranging from simple atomic pairs in a diatomic [[molecule]], to large organic molecules like [[DNA]]. Examples of atomic pairs are two [[nitrogen]] atoms chemically bound to the stable dinitrogen molecule (written as N<sub>2</sub>) and a [[hydrogen]] atom with a [[fluorine]] atom forming [[hydrogen fluoride]] (HF). As an example of larger complexes, [[carbon]] (C) and [[oxygen]] (O) form the pair C—O that appears in many [[Organic chemistry|organic]] molecules, one of the simplest being [[methanol]] H<sub>3</sub>C—OH. Atoms may also be bound to form a [[crystal]], such as [[sodium]] (Na) and chlorine (Cl) that appear in a 1-1 ratio in crystalline rock (kitchen) salt (NaCl). A [[diamond]] crystal can be seen as one huge molecule consisting of bonded C—C (carbon-carbon) pairs. | |||
When dissimilar materials are brought into intimate contact, chemical bonding at the shared interface can occur. It is instrumental in deciding the electrical properties of heterostructures involving [[semiconductor]] materials, for example, as found in the [[Schottky_barrier#Barrier_height|Schottky barrier]]. As another instance, [[reactive dye]]s like [[azo]] and [[formazan]] form washfast covalent bonds with fibres such as cotton. | |||
It took several centuries before chemical bonding was fully understood, but at present it is generally accepted that non-relativistic quantum mechanical explanations based on Coulomb's electrostatic law<ref>That is, explanations derived from quantum mechanical energy operators containing electron-electron, electron-nucleus, and nucleus-nucleus Coulomb interactions plus electronic kinetic energies.</ref> give satisfactory accounts of all kinds of bonds.<ref>As late as 1916 the famous American chemist [[Gilbert Newton Lewis|G. N. Lewis]] disagreed strongly with this statement. He saw electrons as stationary without kinetic energy and not exerting Coulomb forces. In a lecture given at the December meeting of the Sections of Physics and Chemistry of the [[American Association for the Advancement of Science]], the [[American Physical Society]], and the [[American Chemical Society]] (see Science Magazine pp. 297-302 (1917); [http://dx.doi.org/10.1126/science.46.1187.297 DOI]), he declared the following: "Therefore, unless we are willing, under the onslaught of quantum theories, to throw overboard all of the basic principles of physical science, we must conclude that the electron in the Bohr atom not only ceases to obey Coulomb's law, but exerts no influence whatsoever upon another charged particle at any distance." </ref> | |||
Gravitational forces, strong nuclear forces, or even magnetic forces, do not play any significant role in chemical bonding. | Gravitational forces, strong nuclear forces, or even magnetic forces, do not play any significant role in chemical bonding. | ||
==Octet rule== | |||
The octet rule is a simple rule that describes the valency of light atoms ([[atomic number]] ''Z'' ≤ 18, first and second row of the periodic system). The valency of an atom is the number of covalent bonds that the atom can make with a partner. The octet rule starts with the assumption that valency involves only the electrons in the outer [[electron shell|shells]] of the (lowest-energy-state) atoms participating in the bonding. The following lists the number of valence electrons of the first 18 [[chemical elements]] | ==Types of chemical bond== | ||
Traditionally one distinguishes the following types of bonds: | |||
* Covalent bonds (also known as homopolar bonds). A single covalent bond between two atoms is due to an electron pair shared by the atoms. These bonds are very common in [[organic chemistry]]. They occur between, for instance, hydrogen, carbon, nitrogen, and oxygen atoms and give rise to stable, recognizable, molecules. Most covalently bonded molecules remain intact in the solid, liquid, and gaseous [[aggregation state]]s. Covalent bonding requires [[quantum mechanics]] for an explanation and deeper understanding. | |||
* Ionic bonds.<ref>The concept of an ionic bond predates quantum mechanics. In quantum mechanics it is impossible to assign an electron to a definite atom, and the size of an atom in a molecule is not well-defined either. Therefore, quantum chemical methods that compute charges of chemically bound atoms are plagued by a certain amount of arbitrariness. Nevertheless, these calculations show that transfer of a full electronic charge is rare and that occurrences of doubly and triply charged ions in molecules are even rarer. </ref> Here one atom, say A, loses an electron to its bonding partner, call it B. Hence A becomes the [[cation]] A<sup>+</sup> and B the [[anion]] B<sup>−</sup>. Consecutively, the pair A<sup>+</sup>B<sup>−</sup> binds strongly through [[Coulomb's law|Coulomb interaction]]. Systems of which the atoms are bound by ionic interactions are usually crystals, the example of rock salt ({{nowrap|Na<sup>+</sup>—Cl<sup>−</sup>}}) was already mentioned. It requires advanced laboratory techniques to separate ionically bound molecules from crystals, as the crystals are usually very stable. Many ionically bound compounds dissolve in water, dissociating into cations and anions. | |||
* Metallic bonds. A number of metal atoms can crystallize to form a [[metal]], which is a solid recognized by high electric and thermal [[conductivity]]. The bonding is caused by delocalized electrons forming [[Electronic band structure|electronic band]]s. The mechanism is akin to the formation of [[molecular orbital]]s in molecules. An explanation of metallic bonding is offered by quantum mechanics. Metal molecules (M<sub>2</sub>, M<sub>3</sub>, etc.) are not easily prepared experimentally because solid metals are usually very stable. | |||
* Intermolecular (also known as Van der Waals) bonds. These are bonds between stable molecules, see the articles [[intermolecular forces]] and [[Van der Waals forces]] for more details. Bonds between stable molecules are usually a few orders of magnitude (factors 100 to 10 000) weaker than covalent and ionic bonds. For many years it was believed that [[hydrogen bond]]ing was to be classified as a separate type of bond, but modern theoretical chemistry recognizes it as a special type of a (fairly strong) intermolecular bond. | |||
==Covalent bond== | |||
===Octet rule=== | |||
The octet rule is a simple rule that describes the ''valency'' of light atoms ([[atomic number]] ''Z'' ≤ 18, first and second row of the periodic system). The valency of an atom is the number of covalent bonds that the atom can make with a partner. The octet rule starts with the assumption that valency involves only the electrons in the outer [[electron shell|shells]] of the (lowest-energy-state) atoms participating in the bonding. The following lists the number of valence electrons of the first 18 [[chemical elements]] | |||
<div align=center> | <div align=center> | ||
<table width="60%"> | <table width="60%"> | ||
<tr> <td>H(1) <td> He(2) </tr> | <tr> <td>H(1) <td> <td> <td> <td> <td> <td> <td> He(2) </tr> | ||
<tr> <td>Li(1) <td> Be(2) <td> B(3) <td> C(4) <td> N(5) <td> O(6) <td> F(7)<td> Ne(8) </tr> | <tr> <td>Li(1) <td> Be(2) <td> B(3) <td> C(4) <td> N(5) <td> O(6) <td> F(7)<td> Ne(8) </tr> | ||
<tr> <td>Na(1) <td> Mg(2) <td> Al(3) <td> Si(4)<td> P(5) <td> S(6) <td>Cl(7)<td> Ar(8)</tr> | <tr> <td>Na(1) <td> Mg(2) <td> Al(3) <td> Si(4)<td> P(5) <td> S(6) <td>Cl(7)<td> Ar(8)</tr> | ||
</table> | </table> | ||
</div> | </div> | ||
The assumption is that the electron | The assumption is that the electron configurations of noble gases (He, Ne, Ar) are particularly stable (since these gases are chemically inert) and that a bonded atom strives after the configuration of a noble gas near to it in the [[Periodic table of elements|periodic table]]. Except for hydrogen, [[lithium]], [[beryllium]], and [[borium]], which strive for a helium configuration of two electrons (a duplet), it means that most atoms try to surround themselves with an octet of eight electrons. Of course electrons must be shared with bonding partners to achieve such a noble gas configuration. | ||
{{Image|Octet rule.png|right|350px|Examples of octet rule.}} | |||
In the figure four molecules are shown as examples. Both the Lewis representation (electrons as dots) and the corresponding traditional chemical representation (chemical bonds as lines) are shown. In the first molecule (methane, CH<sub>4</sub>) the hydrogen atoms have a helium electronic configuration (are surrounded by two electrons) and the carbon has a neon configuration (is surrounded by an octet consisting of eight electrons). In the computation of the formal charge on the atoms it is assumed that the electrons in a bond are shared equally by the bonding partners. Thus, in methane the hydrogen atoms have one electron, while the carbon atom has four. From the above table it follows that the hydrogens and the carbon are formally electrically neutral in CH<sub>4</sub>. The ethene (formerly known as ethylene) molecule shows a double bond between the carbon atoms. Note that both carbons have a neon configuration (are surrounded by four electron pairs). The next molecule (the nitrogen molecule N<sub>2</sub>) shows a triple bond. Both N-atoms are surrounded by an octet (four electron pairs). Each N-atom has five electrons and is formally neutral. The last molecule (trimethyloxamine) has as central atom a nitrogen atom with four electrons, and hence the nitrogen lacks an electron and has a formal charge +1. The oxygen atom has three pairs to itself and shares one pair, carrying seven electrons, so that oxygen has the formal charge −1. The total trimethyloxamine molecule is neutral. | |||
====Historical note==== | |||
The octet rule is usually attributed to [[Gilbert Newton Lewis]],<ref>G. N. Lewis, ''The Atom and the Molecule'', Journal American Chemical Society, vol. '''38''', pp. 762–785 (1916)</ref> who referred to it as the "rule of eight". The term "octet rule" is due to [[Irving Langmuir]], <ref>I. Langmuir, ''The Arrangement of Electrons in Atoms and Molecules'', Journal American Chemical Society, vol. '''41''', pp. 868–934 (1919)</ref> who extended and refined the work of Lewis. Lewis saw an atom as a cube with—depending on the atom—one to eight valence electrons on its corners. In this picture molecules consist of cubes piled on top of each other, or next to each other sharing a side or a corner. In Ref.<ref>W. B. Jensen, ''Abegg, Lewis, Langmuir, and the octet rule'', Journal Chemical Education, vol. '''61''', pp. 191–200 (1984); [http://dx.doi.org/10.1021/ed061p191 DOI]</ref> it is argued that this idea is not as novel as it is usually believed, but that the idea of the rule of eight was floating among contemporary chemists and that, for instance, the German chemist [[Richard Abegg]] presented already in 1902 some bonding concepts that came close to Lewis's 1916 ideas. In any case, it is generally accepted that Lewis was the first to see the importance of electron pairing. Lewis made the simple assumption that molecules are held together by the pairs of electrons that are shared between bonding atoms and furthermore he assumed that all atomic "kernels" (nuclei plus inner shell electrons) repel one another; at the bond distance the two opposing forces are in equilibrium. | |||
It is remarkable how far physics and chemistry were separated still during the first two decades of the twentieth century. Neither Lewis nor Langmuir put much faith in the [[Ernest Rutherford|Rutherford]]-[[Bohr]] planetary model of the atom in which the negative electrons orbit a positive nucleus. Both chemists believed electrons to be stationary on the vertices of cubic atoms. On the other hand, the founding fathers of quantum mechanical bonding theory (the physicists [[Walter Heitler]], [[Fritz London]], [[Georg Rumer]], [[Edward Teller]], and others) completely ignored the chemists (or perhaps were not even aware of their work). [[Linus Pauling]] deserves the credit for having bridged the two branches of science, which he did in a series of papers in the early 1930s and in his famous 1939 book ''The Nature of the Chemical Bond''<ref>L. Pauling, ''The Nature of the Chemical Bond'', Cornell University Press, 3rd edition, 1960</ref> that is dedicated to G. N. Lewis. In modern chemistry textbooks, chemical bonding theory is usually presented as a continuous development from Lewis's concepts to the Heitler-London theory for the binding in H<sub>2</sub>. Such presentation of the development of ideas is a historic simplification. | |||
==Ionic bond== | |||
Two of the determining factors in the forming of an ionic bond between atoms are the [[ionization energy|ionization energies]] of the atom becoming a cation and the [[electron affinity|electron affinities]] of the atom that receives one or more electrons and becomes an anion. | |||
The ''ionization energy'' is the minimum energy needed to remove an electron from an atom. Ionization energies vary throughout the periodic table; the elements with the lowest ionization energies (from which an electron is most easily removed) are found at the lower left of the periodic table, near [[caesium]] and [[francium]], and elements with the highest ionization energies are found at the upper right of the table, close to [[fluorine]] and [[helium]]. | |||
The noble gases lie on the right of the periodic table, and the members of the family that are closest to helium (namely, [[neon]] and [[argon]]) are among the elements with highest ionization energies, so that their electrons are not readily available for bond formation. For the heavier noble gases, [[krypton]] and [[xenon]], the ionization energies become comparable to those of other elements and indeed these elements exhibit some compound formation. | |||
Elements on the left in the periodic table, which have one, two, or three electrons in their valence shell can lose these valence electrons, but ionization of electrons from inner shells requires so much energy that it will never occur in chemical bonding. Hence, in chemical bonds one may encounter Na<sup>+</sup>, Mg<sup>2+</sup>, and Al<sup>3+</sup>, but not, for instance, Mg<sup>3+</sup>, because this would require removal of an electron from the inner shell of magnesium. In general it costs more energy to remove an electron from a cation than from a neutral atom, which means that the first ionization is smaller (in absolute value) than the second, which is again smaller than the third ionization energy (required to extract an electron from a doubly charged cation). | |||
''Electron affinity'' is the energy change accompanying the attachment of electrons to a neutral atom. It is positive when energy is released upon electron attachment to an atom. This usually happens when an electron occupies an empty orbital in the valence shell of the atom. However, if the incoming electron has to occupy a higher shell because the shells of the neutral atom are filled, then energy must be supplied to attach the electron to form an anion and electron affinity is negative. This is always the case for noble gas atoms. Electron affinities vary through the periodic table, but their periodicity is more complex than that of ionization energies. Electron affinities are generally largest close to the upper right of the periodic table (i.e., near fluorine). | |||
In Lewis's picture, the formation of an ionic bond stems from the transfer of electrons from one atom to another. When such a transfer occurs, all the electrons of an element with low first, second, etc., ionization potentials (on the left in the periodic table) are transferred to the other atom that has high electron affinities (is on the right in the periodic table). The electron-donating atom (the cation) obtains the electron configuration of the noble gas atom to its left and the electron-accepting atom (the anion) gets the configuration of the noble gas atom to its right. For example, the neutral alumina (Al<sub>2</sub>O<sub>3</sub>) has—according to Lewis—the electronic configuration (Al<sup>3+</sup>)<sub>2</sub> (O<sup>2−</sup>)<sub>3</sub>, that is, all atoms have the electron configuration of neutral neon. | |||
Evidently, there is more to the process than a straightforward consideration of ionization energies and electron affinities. When ions bind by Coulomb force, energy is released and this energy must be large enough to overcome the algebraic sum of ionization energies (costs energy) and electron affinities (delivers energy). The Coulomb interaction is inversely proportional to the distance between ions. Thus, it may happen that at large separations the system consisting of neutral atoms has the lowest energy, because the affinities of the free acceptor atom are smaller than the ionization potentials of the free electron-donating atom. However, when the two atoms are brought together, a point may be reached at which the lowest total energy is obtained if an electron transfers from one atom to the other. At this distance, and at shorter distances, the ionic complex is the lower-energy species. | |||
Finally, it was already pointed out above for NaCl that an ionic compound is typically a solid formed from an array of alternating cations and anions. The packing of ions and their electrostatic interactions account for the typical features of ionic compounds, such as their high melting points. | |||
==Theoretical approaches== | |||
To calculate the behavior of the chemical bond the wavefunctions of the electrons must be determined, as these decide how the negative electron charges are arranged among the participating atoms. The wavefunction is found using quantum mechanics, but unfortunately the mathematical formulation is very complex and simplifications are necessary both to render the problem practical and to provide some interpretation of what the calculations mean on an intuitive level that will allow the mind to think about reactions. A number of approaches have evolved to do this. They fall into two main groups related to the way the approximations are introduced. One one hand, the calculation begins with the atoms far apart and with the electrons governed by atomic wavefunctions. The focus is upon the atoms interacting, and is called ''valence bond'' theory. On the other hand, in the ''molecular orbital'' approach, the atomic nuclei are considered as situated at some particular separation creating potential wells for the electrons centered on their cores. The wavefunctions of this potential are found, which is more complicated than it seems as each electron added changes the potential because of its negative charge. | |||
The two methods are not different if carried out to a complete calculation: the difference is in the starting point and in the intuitive notions underlying their beginning approximations. | |||
===Heitler-London theory=== | |||
''See also [[Molecular orbital#Computation of molecular orbitals|molecular orbital]]s for a treatment of the binding in'' H<sub>2</sub>. | |||
{{Image|Heitler London.png|right|450px|Fig. 2. Interaction energy curves as a function of the H—H distance in H<sub>2</sub>. The energy ''E''<sub>0</sub> is of the unsymmetrized wave function, ''E''<sub>+</sub> is of the symmetric wave function, and ''E''<sub>−</sub> is the energy of the antisymmetric wave function. See [[Chemical bond/Code|this page]] for the code that prepared this plot. }} | |||
The first satisfactory explanation of the covalent (homopolar) binding in a diatomic molecule was given by [[Walter Heitler|Heitler]] and [[Fritz London|London]] in 1927,<ref>W. Heitler and F. London ''Wechselwirkung neutraler Atome und homöopolare Bindung nach der Quantenmechanik'' [Interaction between neutral atoms and homopolar binding according to quantum mechanics], Zeitschrift für Physik, vol. '''4''', p. 455–472 (1927). [http://www.quantum-chemistry-history.com/Heitler_London_Dat/WechselWirk1927/WechselWirk1927.htm Original German text]. | |||
English translation: H. Hettema, ''Quantum Chemistry: Classic Scientific Papers'', World Scientific, Singapore (2000). </ref> who used (the then new) [[quantum mechanics]]. They considered the simplest neutral diatomic: the hydrogen molecule. They showed that chemical bonding in this two-electron system was obtained when the indistinguishability of the electrons was accounted for. | |||
It is evident that if the two hydrogen atoms ''A'' and ''B'' are isolated from each other by a large separation, the wavefunction for the two electrons (say electron 1 and electron 2) is simply the product of the two separated wavefunctions, say ψ(1,2) = φ<sub>a</sub>(1)φ<sub>b</sub>(2) because the Hamiltonian for the two atoms is ''H<sub>A</sub> + H<sub>B</sub>''. At close separations, however, ψ(1,2) is only an approximate wavefunction, because ''H<sub>A</sub> + H<sub>B</sub>'' is only approximately the Hamiltonian when electron 1 experiences atom ''B'' and electron 2 experiences atom ''A''. | |||
The symmetry of the physical situation suggests that the same result applies regardless of which electron is chosen as electron 1 and which as electron 2. In other words, ψ(1,2) = ''N''[φ<sub>a</sub>(1)φ<sub>b</sub>(2) + φ<sub>a</sub>(2)φ<sub>b</sub>(1)], with ''N'' a normalization factor to make probabilities using ψ add up to one. However, the wavefunction for two electrons must be ''antisymmetric'' under electron exchange to satisfy the [[Pauli exclusion principle]]. That is made true by choosing the spin part of the wavefunction to flip sign upon exchange of electrons, allowing the spatial part to be symmetric. | |||
The basic idea of Heitler and London was to use this symmetrized product of the wave functions of the separate hydrogen atoms as an approximation to the molecular wave function. If that is done, as the atoms approach each other, the electron density between the positive nucleii is appreciable. Over a range of distances not too small and not too large, the attraction of the two positive nuclei to this intervening electron charge is sufficient to overcome the nuclear repulsion and the hydrogen molecule is stable. | |||
Some mathematical detail follows. | |||
The hydrogen atom wave functions are | |||
:<math> | |||
\phi_a(1) \equiv \sqrt{\frac{1}{a_0^3 \pi}}\; e^{-r_{1\mathrm{A}}/a_0} \quad \hbox{and}\quad | |||
\phi_b(2) \equiv \sqrt{\frac{1}{a_0^3 \pi}}\; e^{-r_{2\mathrm{B}}/a_0} | |||
</math> | |||
where ''r''<sub>1A</sub> is the distance of electron 1 to hydrogen nucleus A. Likewise ''r''<sub>2B</sub> is the distance of electron 2 to nucleus B. The quantity ''a''<sub>0</sub> is the [[Bohr radius]] (= 52.9 pm). The functions are normalized to unity, | |||
:<math> | |||
\int \phi_a(1)^2 \; \mathrm{d}x_{1\mathrm{A}}\mathrm{d}y_{1\mathrm{A}}\mathrm{d}z_{1\mathrm{A}} = | |||
\int \phi_b(2)^2 \; \mathrm{d}x_{2\mathrm{B}}\mathrm{d}y_{2\mathrm{B}}\mathrm{d}z_{2\mathrm{B}} = 1 | |||
</math> | |||
where the integrals are over all of ℝ<sup>3</sup>. The product function is an eigenfunction of the sum of two [[hydrogen-like atom|hydrogen-atom]] Hamiltonians, | |||
:<math> | |||
H^{(0)}\phi_a(1)\phi_b(2) \equiv \left[\Big( -\frac{\hbar^2}{2m_e}\nabla_1^2 - \frac{1}{r_{1\mathrm{A}}}\Big) | |||
+\Big( -\frac{\hbar^2}{2m_e}\nabla_2^2 - \frac{1}{r_{2\mathrm{B}}}\Big)\right]\phi_a(1)\phi_b(2) | |||
= -2E_\mathrm{H} \phi_a(1)\phi_b(2), | |||
</math> | |||
where the electron-nucleus Coulomb interactions are expressed in [[Gaussian units]]. Unit of charge is such that electrons have charge −1 and the hydrogen nuclei +1. The quantity ∇<sup>2</sup> is the [[nabla]] operator squared (acting on the coordinates of electron 1 and 2, respectively); ℏ is [[Planck's constant]] and ''m''<sub>e</sub> is the mass of an [[electron]]. The quantity ''E''<sub>H</sub> is the energy of one free hydrogen atom in its ground state (≈ 13.6 [[electronvolt]]). | |||
The Heitler-London approach is basically first-order [[perturbation theory]], with ''H''<sup>(0)</sup> as unperturbed operator and an interaction (perturbation) operator ''V'' that consists of Coulomb terms only | |||
:<math> | |||
V = -\frac{1}{r_{1\mathrm{B}}}-\frac{1}{r_{2\mathrm{A}}}+\frac{1}{r_{12}} +\frac{1}{R_{\mathrm{AB}}}. | |||
</math> | |||
Here ''R''<sub>AB</sub> is the distance between the nuclei and ''r''<sub>12</sub> is the distance between the electrons. If one interprets φ<sub>a</sub>(1)<sup>2</sup> as the charge distribution of electron 1 and φ<sub>b</sub>(2)<sup>2</sup> of electron 2, the classical electrostatic energy between the two (non-polarizable) charge distributions is | |||
:<math> | |||
E_0(R) \equiv\int\int \phi_a(1)^2 \;V\; \phi_b(2)^2 \; \mathrm{d}x_{1\mathrm{A}}\mathrm{d}y_{1\mathrm{A}}\mathrm{d}z_{1\mathrm{A}}\mathrm{d}x_{2\mathrm{B}}\mathrm{d}y_{2\mathrm{B}}\mathrm{d}z_{2\mathrm{B}}. | |||
</math> | |||
This sixfold integral can be worked out and is a function of ''R'' ≡ ''R''<sub>AB</sub>. The result is shown in figure 2 (red curve). The curve shows a very shallow minimum, far less than the known bonding energy (≈ 104 kcal/mol). For shorter distances the curve is repulsive (has negative slope), which is due to the fact that the nucleus-nucleus repulsion is no longer screened by the electrons. Quantum mechanically, ''E''<sub>0</sub> is the expectation value of the operator ''V'' (first-order energy) with respect to the product wave function φ<sub>a</sub>(1)φ<sub>b</sub>(2). | |||
A deep quantum mechanical principle was ignored so far: ''electrons are indistinguishable particles''. This may also be phrased as: permutations of electrons are symmetry operators. In this two-electron system there are only two permutations: ''I'' ("doing nothing") and ''P'' (interchange of electron 1 and 2). It is known that eigenfunctions of Hamiltonians (which by definition commute with the symmetry operators) are adapted to the symmetry (technically: eigenfunctions belong to irreducible representations of the full symmetry group of the Hamiltonian). In the case at hand this means that H<sub>2</sub> wave functions (eigenfunctions of the H<sub>2</sub> Hamiltonian) have the properties | |||
:<math> | |||
I\psi_\plusmn(1,2) = \psi_\plusmn(1,2)\quad\hbox{and}\quad P\psi_\plusmn(1,2) = \plusmn \psi_\plusmn(1,2) . | |||
</math> | |||
The product wave function that gave rise to the energy ''E''<sub>0</sub> lacks the second symmetry property, and therefore we try new approximate (zeroth-order) wave functions that are symmetry-adapted, | |||
:<math> | |||
\psi_+(1,2) = \sqrt{\frac{1}{2+2S^2}}\;\Big( \phi_a(1)\phi_b(2) + \phi_a(2)\phi_b(1)\Big)\quad\hbox{and}\quad | |||
\psi_-(1,2) = \sqrt{\frac{1}{2-2S^2}}\;\Big( \phi_a(1)\phi_b(2) - \phi_a(2)\phi_b(1)\Big), | |||
</math> | |||
where the ''overlap integral'' ''S'' is given by | |||
:<math> | |||
S(R) = \int \phi_a(1)\phi_b(1) \; \mathrm{d}x_{1\mathrm{A}}\mathrm{d}y_{1\mathrm{A}}\mathrm{d}z_{1\mathrm{A}}. | |||
</math> | |||
Clearly the function ψ<sub>+</sub> is symmetric and ψ<sub>−</sub> is antisymmetric under ''P''. Both functions are normalized to unity thanks to the factors containing the square roots. According to quantum mechanical rules, the following expectation values (first-order energies), derived from properly symmetrized wave functions, give reasonable approximations to the exact energies, | |||
:<math> | |||
E_+(R) \equiv \langle \psi_+ | V| \psi_+ \rangle\quad\hbox{and}\quad | |||
E_-(R) \equiv \langle \psi_- | V| \psi_- \rangle . | |||
</math> | |||
For conciseness the quantum mechanical bra-ket notation is used, for instance, the first braket: | |||
:<math> | |||
\langle \psi_+ | V| \psi_+ \rangle \equiv | |||
\int\int \psi_+(1,2) \;V\; \psi_+(1,2) \; \mathrm{d}x_{1\mathrm{A}}\mathrm{d}y_{1\mathrm{A}}\mathrm{d}z_{1\mathrm{A}}\mathrm{d}x_{2\mathrm{B}}\mathrm{d}y_{2\mathrm{B}}\mathrm{d}z_{2\mathrm{B}}. | |||
</math> | |||
It is not difficult to show that | |||
:<math> | |||
E_\plusmn(R) = \frac{E_0 \plusmn E_{1} }{1\plusmn S^2} | |||
</math> | |||
with | |||
:<math> | |||
E_0(R) = \langle \phi_a(1)\phi_b(2)|V|\phi_a(1)\phi_b(2)\rangle | |||
</math> | |||
and | |||
:<math> | |||
E_1(R) = \langle \phi_a(1)\phi_b(2)|V|\phi_a(2)\phi_b(1)\rangle = | |||
\int\int \phi_a(1)\phi_b(2) \;V\; \phi_b(1)\phi_a(2) \; \mathrm{d}x_{1\mathrm{A}}\mathrm{d}y_{1\mathrm{A}}\mathrm{d}z_{1\mathrm{A}}\mathrm{d}x_{2\mathrm{B}}\mathrm{d}y_{2\mathrm{B}}\mathrm{d}z_{2\mathrm{B}}. | |||
</math> | |||
The energy ''E''<sub>0</sub> was discussed earlier, it arose from classical considerations, and it is small as long as the internuclear repulsion is screened by the electrons. New is the term ''E''<sub>1</sub> which is negative and sizable and the denominator. The presence of ''E''<sub>1</sub>, often referred to as ''exchange term'', has the consequence that ''E''<sub>−</sub> is strongly repulsive for all ''R''-values, while the energy ''E''<sub>+</sub> shows a minimum of 0.232 E<sub>H</sub> (the energy of the hydrogen atom), which is ≈ 73 kcal/mol, about 70% of the exact value. The position of the minimum is at 1.64 a<sub>0</sub> which is not far from the exact value 1.49 a<sub>0</sub>. | |||
It is important to emphasize that the exchange term appears because of the symmetry-adaptation of the zeroth-order wave function. In a classical approach, where electrons are distinguishable, there is no reason to symmetrize and the exchange term does not appear. To give an indication of the orders of magnitude we list the values at 1.60 a<sub>0</sub> (near the minimum): | |||
:S = 0.6972, E<sub>0</sub> = −0.0307, E<sub>1</sub> = −0.3132 | |||
At 1.6 a<sub>0</sub>, the exchange term is an order of magnitude larger than the Coulomb term. | |||
====Remark==== | |||
The Heitler-London theory is often put forward as a proof of the foresight of G. N. Lewis, who stressed the importance of electron pairs for chemical binding. As pointed out by Slater<ref>J. C. Slater, ''Quantum Theory of Molecules and Solids'', vol. 1, McGraw-Hill, New York (1963)</ref> the hydrogen-molecule-cation H<sub>2</sub><sup>+</sup>, which has one electron, is bound by a mechanism that is very similar to the one responsible for binding in H<sub>2</sub>. The main difference is that permutation symmetry is replaced by reflection symmetry. Hence one-electron bonds do exist. | |||
===Relation to electron spin=== | |||
An electron has a spin up (spin function α) or spin down (spin function β). Two electrons can have four spin functions | |||
:<math> | |||
\alpha(1)\alpha(2),\quad\alpha(1)\beta(2),\quad \beta(1)\alpha(2),\quad \beta(1)\beta(2) | |||
</math> | |||
These functions are ''not'' adapted to permutation symmetry. However, the following linear combinations ''are'' adapted | |||
:<math> | |||
\begin{align} | |||
\Theta^0_- &= \alpha(1)\beta(2)- \beta(1)\alpha(2) \\ | |||
\Theta_+^1 &= \alpha(1)\alpha(2) \\ | |||
\Theta_+^0 &= \alpha(1)\beta(2)+ \beta(1)\alpha(2) \\ | |||
\Theta_+^{-1} &=\beta(1)\beta(2) \\ | |||
\end{align} | |||
</math> | |||
It can be shown that these functions are eigenfunctions of the spin [[angular momentum]] operators ''S''<sub>''z''</sub> and ''S''<sup>2</sup>. The one antisymmetric functions is known as a ''singlet function'' and the three symmetric functions are known as ''triplet functions''. | |||
Electrons are [[fermion]]s, which means that their total wave functions (containing spin and space coordinates) must be antisymmetric under permutations. Clearly, the following products of space and spin functions are antisymmetric | |||
:<math> | |||
\begin{align} | |||
\psi_-(1,2) \Theta_+^{m} &\qquad (m=-1,\;0,\; 1) \\ | |||
\psi_+(1,2) \Theta_-^{0} & | |||
\end{align} | |||
</math> | |||
The following products are symmetric (would be valid functions if electrons were [[boson]]s, ''quod non''), | |||
:<math> | |||
\begin{align} | |||
\psi_+(1,2) \Theta_+^{m} &\qquad (m=-1,\;0,\; 1) \\ | |||
\psi_-(1,2) \Theta_-^{0} | |||
\end{align} | |||
</math> | |||
We see that ψ<sub>+</sub> (with energy ''E''<sub>+</sub>) can only occur in conjunction with the spin singlet. The spin singlet state gives binding (sometimes very crudely and bordering to wrong expressed as "opposite spins attract"). The three triplet spin functions combine with ψ<sub>−</sub> (with repulsive energies ''E''<sub>−</sub>). Note that {{nowrap|Θ<sup>0</sup><sub>+</sub>}} also consists of two "opposite spins" and yet combines with the repulsive wave function negating the rule "opposite spins attract". | |||
===Valence bond theory and molecular orbital theory=== | |||
The Heitler-London approach to the bonding in H<sub>2</sub> is the first application of ''valence bond theory'', further developed by [[Linus Pauling]] in the 1930s. Valence bond (VB) theory, accounting for chemical bonding in general molecules, has the great advantage that it stays conceptually much closer to chemical bonds, as they are pictured in the minds of chemists, than its competing method, [[molecular orbital theory| molecular orbital (MO) theory]]. | |||
However, VB theory is orders of magnitude more difficult to implement on a computer than MO theory. Naively, it would be tempting to assume that valence bond wave functions depend only on the electrons that participate in a certain chemical bond. This is not correct, because all ''N'' electrons of a molecule are quantum mechanically indistinguishable and must be handled on equal footing. It is therefore very difficult to translate the Lewis approach—in which certain distinctive pairs of electrons are held responsible for certain bonds—to a consistent quantum mechanical formalism. | |||
In principle, valence bond wave functions must be functions of all ''N'' molecular electrons and must be adapted to the total [[permutation group]] S<sub>''N''</sub> consisting of ''N''! permutations.<ref>Technically: VB functions must carry irreducible representations of S<sub>''N''</sub>.</ref> In H<sub>2</sub> the number of electrons equals two and since S<sub>2</sub> is of order 2, Heitler and London had to consider symmetric and antisymmetric functions only. Clearly, ''N''! rises steeply as function of ''N'' and the number of symmetry types (irreducible representations) rises steeply, too. | |||
Not all symmetry types are allowed, though. In the Heitler-London theory it was seen that singlet spin functions only combine with ''symmetric'' products of atomic orbitals, whereas triplet spin functions only combined with ''antisymmetric'' products of atomic orbitals. This was due to the requirement—first formulated by [[Wolfgang Pauli]]—that the total space-spin wave function be antisymmetric. | |||
There is a mathematical theory, due to [[Issai Schur]], [[Alfred Young]], [[Hermann Weyl]], and others, that generalizes these ideas and connects [[spin]] [[angular momentum]] to permutation symmetry. This mathematical theory enables the construction of all-electron valence bond functions (often referred to as ''valence bond structures'') that have the correct permutation and spin symmetry and are antisymmetric. Furthermore, graphical rules exist to choose linearly independent valence bond structure from the very many that can be constructed. As their name suggests, valence bond structures are in one-to-one correspondence with the usual chemical bonding diagrams. | |||
Hence they have a clear conceptual advantage over their counterparts in MO theory that are the [[configuration interaction|configurational]] wave functions constructed as linear combinations of [[Slater determinant]]s. | |||
A second difficulty in the implementation of valence bond theory on a computer is that valence bond structures, once they have been constructed and a linearly independent set of them has been selected, are composed of antisymmetrized ''N''-electron atomic orbital products. Atomic orbitals on different atoms in a molecule are non-orthogonal. In a typical valence bond calculation it is necessary to evaluate ''N'' electron integrals ("matrix elements") of the molecular energy operator ''H'' ("Hamiltonian"), which is an ''N''-electron operator. Say Φ and Ψ are valence bond structures, then a VB calculation requires calculation of the following integrals, | |||
:<math> | |||
\langle \Phi(1,2,\ldots,N) | H | \Psi(1,2,\ldots,N) \rangle | |||
= \int\cdots\int \Phi(1,2,\ldots,N)^* H \Psi(1,2,\ldots,N) d\tau_1 d\tau_2\cdots d\tau_N, | |||
</math> | |||
where ''d''τ<sub>''k''</sub> ≡ ''dx''<sub>''k''</sub>''dy''<sub>''k''</sub>''dz''<sub>''k''</sub> | |||
is the volume element corresponding to electron ''k'', ''k''=1, …, ''N''. | |||
Due to the antisymmetrization, both Φ and Ψ consist of ''N''! terms, so that the integral consist of (''N''!)<sup>2</sup> terms. In MO theory similar integrals do arise, but there the antisymmetrized products consist of [[molecular orbitals]], which are orthogonal. Due to the orthogonality of the molecular orbitals almost all (''N''!)<sup>2</sup> terms vanish and the ''N''-electron integral is not difficult to compute. However, atomic orbitals being non-orthogonal, in a VB approach practically all | |||
(''N''!)<sup>2</sup> terms survive, which makes the integral very time consuming to evaluate. This problem is known as the ''N-factorial catastrophe''. | |||
There is a final problem that valence bond theory shares with molecular orbital theory. In the precomputer era, when integrals were not computed rigorously, it was believed that computations based on a handful of orbital products would suffice. When it became possible to perform computation with the necessary precision it became clear, in VB as well as in MO theory, that extremely many (hundred thousands to millions) antisymmetrized orbital products must be included to obtain results that can be compared with experimental numbers. Moreover, it was found in VB theory that simple atomic orbitals, taken from the free atoms, did not behave as expected. Often atomic orbitals must be prepared in certain ways to function properly in a molecular valence bond calculation. | |||
== | ==Notes== | ||
{{reflist}}[[Category:Suggestion Bot Tag]] | |||
Latest revision as of 11:00, 27 July 2024
For further discussion, see also Theoretical chemistry and Quantum chemistry.
In chemistry, a chemical bond is an arrangement of electrons among atoms that keeps the atoms together. The bond originates in the electrical attraction of opposite charges, and is made possible by the attraction of the positive nucleii of atoms to the electrons associated with them. The central issue in understanding the bond is finding how the electrons associated with atoms distribute their negative charge so as to overcome the natural repulsion between positive atomic cores. A useful understanding can range from an entirely qualitative model based upon the attraction of one atom for electrons compared to another (their electronegativity) to very detailed computer calculations based upon quantum mechanics.
If the total energy of two or more bound atoms is lower than the sum of the energies of the free component atoms, the aggregate of atoms form a stable molecule (or crystal) and the energy lowering is the binding energy of the molecule (or crystal).
The chemical bond takes on many forms, ranging from simple atomic pairs in a diatomic molecule, to large organic molecules like DNA. Examples of atomic pairs are two nitrogen atoms chemically bound to the stable dinitrogen molecule (written as N2) and a hydrogen atom with a fluorine atom forming hydrogen fluoride (HF). As an example of larger complexes, carbon (C) and oxygen (O) form the pair C—O that appears in many organic molecules, one of the simplest being methanol H3C—OH. Atoms may also be bound to form a crystal, such as sodium (Na) and chlorine (Cl) that appear in a 1-1 ratio in crystalline rock (kitchen) salt (NaCl). A diamond crystal can be seen as one huge molecule consisting of bonded C—C (carbon-carbon) pairs.
When dissimilar materials are brought into intimate contact, chemical bonding at the shared interface can occur. It is instrumental in deciding the electrical properties of heterostructures involving semiconductor materials, for example, as found in the Schottky barrier. As another instance, reactive dyes like azo and formazan form washfast covalent bonds with fibres such as cotton.
It took several centuries before chemical bonding was fully understood, but at present it is generally accepted that non-relativistic quantum mechanical explanations based on Coulomb's electrostatic law[1] give satisfactory accounts of all kinds of bonds.[2] Gravitational forces, strong nuclear forces, or even magnetic forces, do not play any significant role in chemical bonding.
Types of chemical bond
Traditionally one distinguishes the following types of bonds:
- Covalent bonds (also known as homopolar bonds). A single covalent bond between two atoms is due to an electron pair shared by the atoms. These bonds are very common in organic chemistry. They occur between, for instance, hydrogen, carbon, nitrogen, and oxygen atoms and give rise to stable, recognizable, molecules. Most covalently bonded molecules remain intact in the solid, liquid, and gaseous aggregation states. Covalent bonding requires quantum mechanics for an explanation and deeper understanding.
- Ionic bonds.[3] Here one atom, say A, loses an electron to its bonding partner, call it B. Hence A becomes the cation A+ and B the anion B−. Consecutively, the pair A+B− binds strongly through Coulomb interaction. Systems of which the atoms are bound by ionic interactions are usually crystals, the example of rock salt (Na+—Cl−) was already mentioned. It requires advanced laboratory techniques to separate ionically bound molecules from crystals, as the crystals are usually very stable. Many ionically bound compounds dissolve in water, dissociating into cations and anions.
- Metallic bonds. A number of metal atoms can crystallize to form a metal, which is a solid recognized by high electric and thermal conductivity. The bonding is caused by delocalized electrons forming electronic bands. The mechanism is akin to the formation of molecular orbitals in molecules. An explanation of metallic bonding is offered by quantum mechanics. Metal molecules (M2, M3, etc.) are not easily prepared experimentally because solid metals are usually very stable.
- Intermolecular (also known as Van der Waals) bonds. These are bonds between stable molecules, see the articles intermolecular forces and Van der Waals forces for more details. Bonds between stable molecules are usually a few orders of magnitude (factors 100 to 10 000) weaker than covalent and ionic bonds. For many years it was believed that hydrogen bonding was to be classified as a separate type of bond, but modern theoretical chemistry recognizes it as a special type of a (fairly strong) intermolecular bond.
Covalent bond
Octet rule
The octet rule is a simple rule that describes the valency of light atoms (atomic number Z ≤ 18, first and second row of the periodic system). The valency of an atom is the number of covalent bonds that the atom can make with a partner. The octet rule starts with the assumption that valency involves only the electrons in the outer shells of the (lowest-energy-state) atoms participating in the bonding. The following lists the number of valence electrons of the first 18 chemical elements
| H(1) | He(2) | ||||||
| Li(1) | Be(2) | B(3) | C(4) | N(5) | O(6) | F(7) | Ne(8) |
| Na(1) | Mg(2) | Al(3) | Si(4) | P(5) | S(6) | Cl(7) | Ar(8) |
The assumption is that the electron configurations of noble gases (He, Ne, Ar) are particularly stable (since these gases are chemically inert) and that a bonded atom strives after the configuration of a noble gas near to it in the periodic table. Except for hydrogen, lithium, beryllium, and borium, which strive for a helium configuration of two electrons (a duplet), it means that most atoms try to surround themselves with an octet of eight electrons. Of course electrons must be shared with bonding partners to achieve such a noble gas configuration.
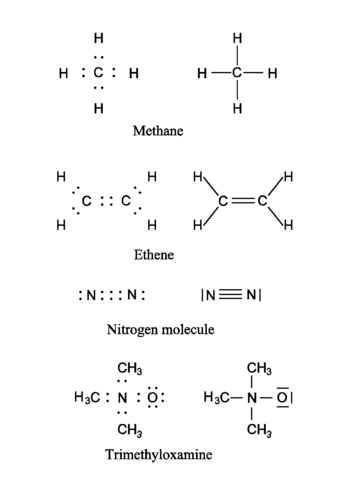
In the figure four molecules are shown as examples. Both the Lewis representation (electrons as dots) and the corresponding traditional chemical representation (chemical bonds as lines) are shown. In the first molecule (methane, CH4) the hydrogen atoms have a helium electronic configuration (are surrounded by two electrons) and the carbon has a neon configuration (is surrounded by an octet consisting of eight electrons). In the computation of the formal charge on the atoms it is assumed that the electrons in a bond are shared equally by the bonding partners. Thus, in methane the hydrogen atoms have one electron, while the carbon atom has four. From the above table it follows that the hydrogens and the carbon are formally electrically neutral in CH4. The ethene (formerly known as ethylene) molecule shows a double bond between the carbon atoms. Note that both carbons have a neon configuration (are surrounded by four electron pairs). The next molecule (the nitrogen molecule N2) shows a triple bond. Both N-atoms are surrounded by an octet (four electron pairs). Each N-atom has five electrons and is formally neutral. The last molecule (trimethyloxamine) has as central atom a nitrogen atom with four electrons, and hence the nitrogen lacks an electron and has a formal charge +1. The oxygen atom has three pairs to itself and shares one pair, carrying seven electrons, so that oxygen has the formal charge −1. The total trimethyloxamine molecule is neutral.
Historical note
The octet rule is usually attributed to Gilbert Newton Lewis,[4] who referred to it as the "rule of eight". The term "octet rule" is due to Irving Langmuir, [5] who extended and refined the work of Lewis. Lewis saw an atom as a cube with—depending on the atom—one to eight valence electrons on its corners. In this picture molecules consist of cubes piled on top of each other, or next to each other sharing a side or a corner. In Ref.[6] it is argued that this idea is not as novel as it is usually believed, but that the idea of the rule of eight was floating among contemporary chemists and that, for instance, the German chemist Richard Abegg presented already in 1902 some bonding concepts that came close to Lewis's 1916 ideas. In any case, it is generally accepted that Lewis was the first to see the importance of electron pairing. Lewis made the simple assumption that molecules are held together by the pairs of electrons that are shared between bonding atoms and furthermore he assumed that all atomic "kernels" (nuclei plus inner shell electrons) repel one another; at the bond distance the two opposing forces are in equilibrium.
It is remarkable how far physics and chemistry were separated still during the first two decades of the twentieth century. Neither Lewis nor Langmuir put much faith in the Rutherford-Bohr planetary model of the atom in which the negative electrons orbit a positive nucleus. Both chemists believed electrons to be stationary on the vertices of cubic atoms. On the other hand, the founding fathers of quantum mechanical bonding theory (the physicists Walter Heitler, Fritz London, Georg Rumer, Edward Teller, and others) completely ignored the chemists (or perhaps were not even aware of their work). Linus Pauling deserves the credit for having bridged the two branches of science, which he did in a series of papers in the early 1930s and in his famous 1939 book The Nature of the Chemical Bond[7] that is dedicated to G. N. Lewis. In modern chemistry textbooks, chemical bonding theory is usually presented as a continuous development from Lewis's concepts to the Heitler-London theory for the binding in H2. Such presentation of the development of ideas is a historic simplification.
Ionic bond
Two of the determining factors in the forming of an ionic bond between atoms are the ionization energies of the atom becoming a cation and the electron affinities of the atom that receives one or more electrons and becomes an anion.
The ionization energy is the minimum energy needed to remove an electron from an atom. Ionization energies vary throughout the periodic table; the elements with the lowest ionization energies (from which an electron is most easily removed) are found at the lower left of the periodic table, near caesium and francium, and elements with the highest ionization energies are found at the upper right of the table, close to fluorine and helium.
The noble gases lie on the right of the periodic table, and the members of the family that are closest to helium (namely, neon and argon) are among the elements with highest ionization energies, so that their electrons are not readily available for bond formation. For the heavier noble gases, krypton and xenon, the ionization energies become comparable to those of other elements and indeed these elements exhibit some compound formation.
Elements on the left in the periodic table, which have one, two, or three electrons in their valence shell can lose these valence electrons, but ionization of electrons from inner shells requires so much energy that it will never occur in chemical bonding. Hence, in chemical bonds one may encounter Na+, Mg2+, and Al3+, but not, for instance, Mg3+, because this would require removal of an electron from the inner shell of magnesium. In general it costs more energy to remove an electron from a cation than from a neutral atom, which means that the first ionization is smaller (in absolute value) than the second, which is again smaller than the third ionization energy (required to extract an electron from a doubly charged cation).
Electron affinity is the energy change accompanying the attachment of electrons to a neutral atom. It is positive when energy is released upon electron attachment to an atom. This usually happens when an electron occupies an empty orbital in the valence shell of the atom. However, if the incoming electron has to occupy a higher shell because the shells of the neutral atom are filled, then energy must be supplied to attach the electron to form an anion and electron affinity is negative. This is always the case for noble gas atoms. Electron affinities vary through the periodic table, but their periodicity is more complex than that of ionization energies. Electron affinities are generally largest close to the upper right of the periodic table (i.e., near fluorine).
In Lewis's picture, the formation of an ionic bond stems from the transfer of electrons from one atom to another. When such a transfer occurs, all the electrons of an element with low first, second, etc., ionization potentials (on the left in the periodic table) are transferred to the other atom that has high electron affinities (is on the right in the periodic table). The electron-donating atom (the cation) obtains the electron configuration of the noble gas atom to its left and the electron-accepting atom (the anion) gets the configuration of the noble gas atom to its right. For example, the neutral alumina (Al2O3) has—according to Lewis—the electronic configuration (Al3+)2 (O2−)3, that is, all atoms have the electron configuration of neutral neon.
Evidently, there is more to the process than a straightforward consideration of ionization energies and electron affinities. When ions bind by Coulomb force, energy is released and this energy must be large enough to overcome the algebraic sum of ionization energies (costs energy) and electron affinities (delivers energy). The Coulomb interaction is inversely proportional to the distance between ions. Thus, it may happen that at large separations the system consisting of neutral atoms has the lowest energy, because the affinities of the free acceptor atom are smaller than the ionization potentials of the free electron-donating atom. However, when the two atoms are brought together, a point may be reached at which the lowest total energy is obtained if an electron transfers from one atom to the other. At this distance, and at shorter distances, the ionic complex is the lower-energy species.
Finally, it was already pointed out above for NaCl that an ionic compound is typically a solid formed from an array of alternating cations and anions. The packing of ions and their electrostatic interactions account for the typical features of ionic compounds, such as their high melting points.
Theoretical approaches
To calculate the behavior of the chemical bond the wavefunctions of the electrons must be determined, as these decide how the negative electron charges are arranged among the participating atoms. The wavefunction is found using quantum mechanics, but unfortunately the mathematical formulation is very complex and simplifications are necessary both to render the problem practical and to provide some interpretation of what the calculations mean on an intuitive level that will allow the mind to think about reactions. A number of approaches have evolved to do this. They fall into two main groups related to the way the approximations are introduced. One one hand, the calculation begins with the atoms far apart and with the electrons governed by atomic wavefunctions. The focus is upon the atoms interacting, and is called valence bond theory. On the other hand, in the molecular orbital approach, the atomic nuclei are considered as situated at some particular separation creating potential wells for the electrons centered on their cores. The wavefunctions of this potential are found, which is more complicated than it seems as each electron added changes the potential because of its negative charge.
The two methods are not different if carried out to a complete calculation: the difference is in the starting point and in the intuitive notions underlying their beginning approximations.
Heitler-London theory
See also molecular orbitals for a treatment of the binding in H2.
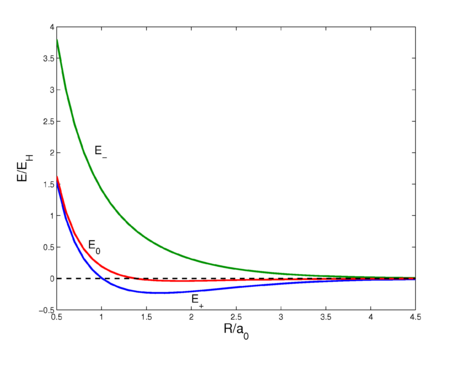
Fig. 2. Interaction energy curves as a function of the H—H distance in H2. The energy E0 is of the unsymmetrized wave function, E+ is of the symmetric wave function, and E− is the energy of the antisymmetric wave function. See this page for the code that prepared this plot.
The first satisfactory explanation of the covalent (homopolar) binding in a diatomic molecule was given by Heitler and London in 1927,[8] who used (the then new) quantum mechanics. They considered the simplest neutral diatomic: the hydrogen molecule. They showed that chemical bonding in this two-electron system was obtained when the indistinguishability of the electrons was accounted for.
It is evident that if the two hydrogen atoms A and B are isolated from each other by a large separation, the wavefunction for the two electrons (say electron 1 and electron 2) is simply the product of the two separated wavefunctions, say ψ(1,2) = φa(1)φb(2) because the Hamiltonian for the two atoms is HA + HB. At close separations, however, ψ(1,2) is only an approximate wavefunction, because HA + HB is only approximately the Hamiltonian when electron 1 experiences atom B and electron 2 experiences atom A.
The symmetry of the physical situation suggests that the same result applies regardless of which electron is chosen as electron 1 and which as electron 2. In other words, ψ(1,2) = N[φa(1)φb(2) + φa(2)φb(1)], with N a normalization factor to make probabilities using ψ add up to one. However, the wavefunction for two electrons must be antisymmetric under electron exchange to satisfy the Pauli exclusion principle. That is made true by choosing the spin part of the wavefunction to flip sign upon exchange of electrons, allowing the spatial part to be symmetric.
The basic idea of Heitler and London was to use this symmetrized product of the wave functions of the separate hydrogen atoms as an approximation to the molecular wave function. If that is done, as the atoms approach each other, the electron density between the positive nucleii is appreciable. Over a range of distances not too small and not too large, the attraction of the two positive nuclei to this intervening electron charge is sufficient to overcome the nuclear repulsion and the hydrogen molecule is stable.
Some mathematical detail follows.
The hydrogen atom wave functions are
where r1A is the distance of electron 1 to hydrogen nucleus A. Likewise r2B is the distance of electron 2 to nucleus B. The quantity a0 is the Bohr radius (= 52.9 pm). The functions are normalized to unity,
where the integrals are over all of ℝ3. The product function is an eigenfunction of the sum of two hydrogen-atom Hamiltonians,
where the electron-nucleus Coulomb interactions are expressed in Gaussian units. Unit of charge is such that electrons have charge −1 and the hydrogen nuclei +1. The quantity ∇2 is the nabla operator squared (acting on the coordinates of electron 1 and 2, respectively); ℏ is Planck's constant and me is the mass of an electron. The quantity EH is the energy of one free hydrogen atom in its ground state (≈ 13.6 electronvolt).
The Heitler-London approach is basically first-order perturbation theory, with H(0) as unperturbed operator and an interaction (perturbation) operator V that consists of Coulomb terms only
Here RAB is the distance between the nuclei and r12 is the distance between the electrons. If one interprets φa(1)2 as the charge distribution of electron 1 and φb(2)2 of electron 2, the classical electrostatic energy between the two (non-polarizable) charge distributions is
This sixfold integral can be worked out and is a function of R ≡ RAB. The result is shown in figure 2 (red curve). The curve shows a very shallow minimum, far less than the known bonding energy (≈ 104 kcal/mol). For shorter distances the curve is repulsive (has negative slope), which is due to the fact that the nucleus-nucleus repulsion is no longer screened by the electrons. Quantum mechanically, E0 is the expectation value of the operator V (first-order energy) with respect to the product wave function φa(1)φb(2).
A deep quantum mechanical principle was ignored so far: electrons are indistinguishable particles. This may also be phrased as: permutations of electrons are symmetry operators. In this two-electron system there are only two permutations: I ("doing nothing") and P (interchange of electron 1 and 2). It is known that eigenfunctions of Hamiltonians (which by definition commute with the symmetry operators) are adapted to the symmetry (technically: eigenfunctions belong to irreducible representations of the full symmetry group of the Hamiltonian). In the case at hand this means that H2 wave functions (eigenfunctions of the H2 Hamiltonian) have the properties
The product wave function that gave rise to the energy E0 lacks the second symmetry property, and therefore we try new approximate (zeroth-order) wave functions that are symmetry-adapted,
where the overlap integral S is given by
Clearly the function ψ+ is symmetric and ψ− is antisymmetric under P. Both functions are normalized to unity thanks to the factors containing the square roots. According to quantum mechanical rules, the following expectation values (first-order energies), derived from properly symmetrized wave functions, give reasonable approximations to the exact energies,
For conciseness the quantum mechanical bra-ket notation is used, for instance, the first braket:
It is not difficult to show that
with
and
The energy E0 was discussed earlier, it arose from classical considerations, and it is small as long as the internuclear repulsion is screened by the electrons. New is the term E1 which is negative and sizable and the denominator. The presence of E1, often referred to as exchange term, has the consequence that E− is strongly repulsive for all R-values, while the energy E+ shows a minimum of 0.232 EH (the energy of the hydrogen atom), which is ≈ 73 kcal/mol, about 70% of the exact value. The position of the minimum is at 1.64 a0 which is not far from the exact value 1.49 a0.
It is important to emphasize that the exchange term appears because of the symmetry-adaptation of the zeroth-order wave function. In a classical approach, where electrons are distinguishable, there is no reason to symmetrize and the exchange term does not appear. To give an indication of the orders of magnitude we list the values at 1.60 a0 (near the minimum):
- S = 0.6972, E0 = −0.0307, E1 = −0.3132
At 1.6 a0, the exchange term is an order of magnitude larger than the Coulomb term.
Remark
The Heitler-London theory is often put forward as a proof of the foresight of G. N. Lewis, who stressed the importance of electron pairs for chemical binding. As pointed out by Slater[9] the hydrogen-molecule-cation H2+, which has one electron, is bound by a mechanism that is very similar to the one responsible for binding in H2. The main difference is that permutation symmetry is replaced by reflection symmetry. Hence one-electron bonds do exist.
Relation to electron spin
An electron has a spin up (spin function α) or spin down (spin function β). Two electrons can have four spin functions
These functions are not adapted to permutation symmetry. However, the following linear combinations are adapted
It can be shown that these functions are eigenfunctions of the spin angular momentum operators Sz and S2. The one antisymmetric functions is known as a singlet function and the three symmetric functions are known as triplet functions.
Electrons are fermions, which means that their total wave functions (containing spin and space coordinates) must be antisymmetric under permutations. Clearly, the following products of space and spin functions are antisymmetric
The following products are symmetric (would be valid functions if electrons were bosons, quod non),
We see that ψ+ (with energy E+) can only occur in conjunction with the spin singlet. The spin singlet state gives binding (sometimes very crudely and bordering to wrong expressed as "opposite spins attract"). The three triplet spin functions combine with ψ− (with repulsive energies E−). Note that Θ0+ also consists of two "opposite spins" and yet combines with the repulsive wave function negating the rule "opposite spins attract".
Valence bond theory and molecular orbital theory
The Heitler-London approach to the bonding in H2 is the first application of valence bond theory, further developed by Linus Pauling in the 1930s. Valence bond (VB) theory, accounting for chemical bonding in general molecules, has the great advantage that it stays conceptually much closer to chemical bonds, as they are pictured in the minds of chemists, than its competing method, molecular orbital (MO) theory.
However, VB theory is orders of magnitude more difficult to implement on a computer than MO theory. Naively, it would be tempting to assume that valence bond wave functions depend only on the electrons that participate in a certain chemical bond. This is not correct, because all N electrons of a molecule are quantum mechanically indistinguishable and must be handled on equal footing. It is therefore very difficult to translate the Lewis approach—in which certain distinctive pairs of electrons are held responsible for certain bonds—to a consistent quantum mechanical formalism. In principle, valence bond wave functions must be functions of all N molecular electrons and must be adapted to the total permutation group SN consisting of N! permutations.[10] In H2 the number of electrons equals two and since S2 is of order 2, Heitler and London had to consider symmetric and antisymmetric functions only. Clearly, N! rises steeply as function of N and the number of symmetry types (irreducible representations) rises steeply, too.
Not all symmetry types are allowed, though. In the Heitler-London theory it was seen that singlet spin functions only combine with symmetric products of atomic orbitals, whereas triplet spin functions only combined with antisymmetric products of atomic orbitals. This was due to the requirement—first formulated by Wolfgang Pauli—that the total space-spin wave function be antisymmetric. There is a mathematical theory, due to Issai Schur, Alfred Young, Hermann Weyl, and others, that generalizes these ideas and connects spin angular momentum to permutation symmetry. This mathematical theory enables the construction of all-electron valence bond functions (often referred to as valence bond structures) that have the correct permutation and spin symmetry and are antisymmetric. Furthermore, graphical rules exist to choose linearly independent valence bond structure from the very many that can be constructed. As their name suggests, valence bond structures are in one-to-one correspondence with the usual chemical bonding diagrams. Hence they have a clear conceptual advantage over their counterparts in MO theory that are the configurational wave functions constructed as linear combinations of Slater determinants.
A second difficulty in the implementation of valence bond theory on a computer is that valence bond structures, once they have been constructed and a linearly independent set of them has been selected, are composed of antisymmetrized N-electron atomic orbital products. Atomic orbitals on different atoms in a molecule are non-orthogonal. In a typical valence bond calculation it is necessary to evaluate N electron integrals ("matrix elements") of the molecular energy operator H ("Hamiltonian"), which is an N-electron operator. Say Φ and Ψ are valence bond structures, then a VB calculation requires calculation of the following integrals,
where dτk ≡ dxkdykdzk is the volume element corresponding to electron k, k=1, …, N. Due to the antisymmetrization, both Φ and Ψ consist of N! terms, so that the integral consist of (N!)2 terms. In MO theory similar integrals do arise, but there the antisymmetrized products consist of molecular orbitals, which are orthogonal. Due to the orthogonality of the molecular orbitals almost all (N!)2 terms vanish and the N-electron integral is not difficult to compute. However, atomic orbitals being non-orthogonal, in a VB approach practically all (N!)2 terms survive, which makes the integral very time consuming to evaluate. This problem is known as the N-factorial catastrophe.
There is a final problem that valence bond theory shares with molecular orbital theory. In the precomputer era, when integrals were not computed rigorously, it was believed that computations based on a handful of orbital products would suffice. When it became possible to perform computation with the necessary precision it became clear, in VB as well as in MO theory, that extremely many (hundred thousands to millions) antisymmetrized orbital products must be included to obtain results that can be compared with experimental numbers. Moreover, it was found in VB theory that simple atomic orbitals, taken from the free atoms, did not behave as expected. Often atomic orbitals must be prepared in certain ways to function properly in a molecular valence bond calculation.
Notes
- ↑ That is, explanations derived from quantum mechanical energy operators containing electron-electron, electron-nucleus, and nucleus-nucleus Coulomb interactions plus electronic kinetic energies.
- ↑ As late as 1916 the famous American chemist G. N. Lewis disagreed strongly with this statement. He saw electrons as stationary without kinetic energy and not exerting Coulomb forces. In a lecture given at the December meeting of the Sections of Physics and Chemistry of the American Association for the Advancement of Science, the American Physical Society, and the American Chemical Society (see Science Magazine pp. 297-302 (1917); DOI), he declared the following: "Therefore, unless we are willing, under the onslaught of quantum theories, to throw overboard all of the basic principles of physical science, we must conclude that the electron in the Bohr atom not only ceases to obey Coulomb's law, but exerts no influence whatsoever upon another charged particle at any distance."
- ↑ The concept of an ionic bond predates quantum mechanics. In quantum mechanics it is impossible to assign an electron to a definite atom, and the size of an atom in a molecule is not well-defined either. Therefore, quantum chemical methods that compute charges of chemically bound atoms are plagued by a certain amount of arbitrariness. Nevertheless, these calculations show that transfer of a full electronic charge is rare and that occurrences of doubly and triply charged ions in molecules are even rarer.
- ↑ G. N. Lewis, The Atom and the Molecule, Journal American Chemical Society, vol. 38, pp. 762–785 (1916)
- ↑ I. Langmuir, The Arrangement of Electrons in Atoms and Molecules, Journal American Chemical Society, vol. 41, pp. 868–934 (1919)
- ↑ W. B. Jensen, Abegg, Lewis, Langmuir, and the octet rule, Journal Chemical Education, vol. 61, pp. 191–200 (1984); DOI
- ↑ L. Pauling, The Nature of the Chemical Bond, Cornell University Press, 3rd edition, 1960
- ↑ W. Heitler and F. London Wechselwirkung neutraler Atome und homöopolare Bindung nach der Quantenmechanik [Interaction between neutral atoms and homopolar binding according to quantum mechanics], Zeitschrift für Physik, vol. 4, p. 455–472 (1927). Original German text. English translation: H. Hettema, Quantum Chemistry: Classic Scientific Papers, World Scientific, Singapore (2000).
- ↑ J. C. Slater, Quantum Theory of Molecules and Solids, vol. 1, McGraw-Hill, New York (1963)
- ↑ Technically: VB functions must carry irreducible representations of SN.


![{\displaystyle H^{(0)}\phi _{a}(1)\phi _{b}(2)\equiv \left[{\Big (}-{\frac {\hbar ^{2}}{2m_{e}}}\nabla _{1}^{2}-{\frac {1}{r_{1\mathrm {A} }}}{\Big )}+{\Big (}-{\frac {\hbar ^{2}}{2m_{e}}}\nabla _{2}^{2}-{\frac {1}{r_{2\mathrm {B} }}}{\Big )}\right]\phi _{a}(1)\phi _{b}(2)=-2E_{\mathrm {H} }\phi _{a}(1)\phi _{b}(2),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd5dc72403e21d932055157cfed5dad8b88e4b7e)














