Parallax: Difference between revisions
imported>Paul Wormer No edit summary |
imported>Paul Wormer |
||
| Line 3: | Line 3: | ||
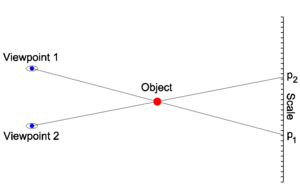
[[Image:Parallax.png|right|thumb|300px|Fig. 1: An observer at viewpoint 1 measures the object to be at p<sub>1</sub> on the scale and an observer at viewpoint 2 measures it at p<sub>2</sub>. The distance p<sub>2</sub>−p<sub>1</sub> is the (linear) parallax. ]] | [[Image:Parallax.png|right|thumb|300px|Fig. 1: An observer at viewpoint 1 measures the object to be at p<sub>1</sub> on the scale and an observer at viewpoint 2 measures it at p<sub>2</sub>. The distance p<sub>2</sub>−p<sub>1</sub> is the (linear) parallax. ]] | ||
==Diurnal parallax== | ==Diurnal parallax== | ||
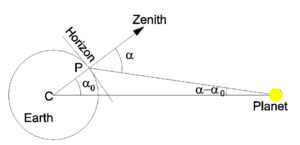
In [[astronomy]], the '''diurnal parallax''' is the parallax caused by the diurnal (daily) rotation of the Earth. In Fig. 2, an observer at ''P'' sees the surface of the Earth as a plane bounded by the horizon. Perpendicular to the plane is the [[zenith]]. The observer observes the | In [[astronomy]], the '''diurnal parallax''' is the parallax caused by the diurnal (daily) rotation of the Earth. In Fig. 2, an observer at ''P'' sees the surface of the Earth as a plane bounded by the horizon. Perpendicular to the plane is the [[zenith]]. The observer observes a planet (or the Moon or the Sun) under an angle α with the zenith, this angle is the ''topocentric zenith distance'' of the planet. The angle can be determined, for instance, against the background of fixed stars. Similarly, the angle α<sub>0</sub> is the ''geocentric zenith distance'' (measured from ''C'', the center of the Earth). The diurnal parallax is the angle α−α<sub>0</sub>. Note that the diurnal parallax is zero when the planet is in the zenith (above the observer at ''P''); both α and α<sub>0</sub> are zero. When the planet is at the horizon the diurnal parallax is maximum. When the planet is under the horizon the star cannot be observed at ''P''. Fig. 2 illustrates a theorem known from high-school geometry: any exterior angle of a triangle is equal to the sum of the two interior and opposite angles. | ||
[[Image:Diurnal parallax.png|left|thumb|300px|Fig. 2: Diurnal parallax is the angle α−α<sub>0</sub>.]] | [[Image:Diurnal parallax.png|left|thumb|300px|Fig. 2: Diurnal parallax is the angle α−α<sub>0</sub>.]] | ||
Revision as of 07:20, 16 October 2008
Parallax is the apparent change in the position of an object resulting from a change in position of the observer, see Fig. 1.
Diurnal parallax
In astronomy, the diurnal parallax is the parallax caused by the diurnal (daily) rotation of the Earth. In Fig. 2, an observer at P sees the surface of the Earth as a plane bounded by the horizon. Perpendicular to the plane is the zenith. The observer observes a planet (or the Moon or the Sun) under an angle α with the zenith, this angle is the topocentric zenith distance of the planet. The angle can be determined, for instance, against the background of fixed stars. Similarly, the angle α0 is the geocentric zenith distance (measured from C, the center of the Earth). The diurnal parallax is the angle α−α0. Note that the diurnal parallax is zero when the planet is in the zenith (above the observer at P); both α and α0 are zero. When the planet is at the horizon the diurnal parallax is maximum. When the planet is under the horizon the star cannot be observed at P. Fig. 2 illustrates a theorem known from high-school geometry: any exterior angle of a triangle is equal to the sum of the two interior and opposite angles.