Harmonic oscillator (quantum): Difference between revisions
imported>Paul Wormer No edit summary |
imported>Paul Wormer No edit summary |
||
| Line 24: | Line 24: | ||
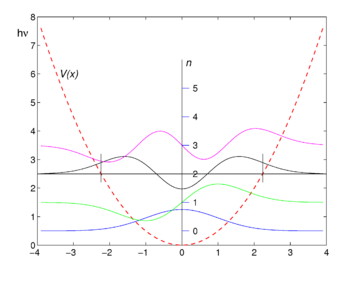
The graphs of the first four eigenfunctions are shown in the figure. Note that the functions of even ''n'' are even, that is, <math>f_{2n}(-x) = f_{2n}(x)\,</math>, while those of odd ''n'' are antisymmetric <math>f_{2n+1}(-x) = - f_{2n+1}(x)\,.</math> | The graphs of the first four eigenfunctions are shown in the figure. Note that the functions of even ''n'' are even, that is, <math>f_{2n}(-x) = f_{2n}(x)\,</math>, while those of odd ''n'' are antisymmetric <math>f_{2n+1}(-x) = - f_{2n+1}(x)\,.</math> | ||
==Solution of the Schrödinger equation== | |||
We rewrite the Schrödinger equation so as to hide the physical constants ''m'', ''k'', and ''h''. As a first step we define the angular frequency ω ≡ √''k''/''m'', the same formula as for the classical harmonic oscillator: | |||
:<math> | |||
\frac{1}{2}\left[-\frac{\hbar^2}{m}\frac{\mathrm{d}^2}{\mathrm{d}x^2} + m\omega^2 x^2\right] \psi = E\psi. | |||
</math> | |||
Secondly, we divide through by <math>\hbar\omega</math>, a factor that has dimension energy, | |||
:<math> | |||
\frac{1}{2}\left[-\frac{\hbar}{m\omega}\frac{\mathrm{d}^2}{\mathrm{d}x^2} + \frac{m\omega}{\hbar} x^2\right] \psi = \frac{E}{\hbar\omega}\psi. | |||
</math> | |||
Write | |||
:<math> \beta \equiv \sqrt{\frac{m\omega}{\hbar}}, \quad y \equiv \beta x, \quad \mathcal{E}\equiv \frac{E}{\hbar\omega} | |||
</math> | |||
and the Schrödinger equation becomes | |||
:<math> | |||
\frac{1}{2}\left[- \frac{1}{\beta^2}\frac{\mathrm{d}^2}{\mathrm{d}x^2} + \beta^2 x^2\right] \psi = \mathcal{E}\psi\quad \Longrightarrow\quad | |||
\frac{1}{2}\left[-\frac{\mathrm{d}^2}{\mathrm{d}y^2} + y^2\right] \psi = \mathcal{E} \psi. | |||
</math> | |||
Note that all constants are out of sight in the equation on the right. | |||
A particular solution of this equation is | |||
:<math> | |||
\psi_0(y) = e^{-y^2/2}. | |||
</math> | |||
We verify this | |||
:<math> | |||
-\frac{\mathrm{d}e^{-y^2/2}}{\mathrm{d}y} = y e^{-y^2/2} | |||
\quad\hbox{and}\quad \frac{\mathrm{d}(y e^{-y^2/2})}{\mathrm{d}y}= | |||
e^{-y^2/2}\left(1 - y^2\right), | |||
</math> | |||
so that | |||
:<math> | |||
\frac{1}{2}\left[-\frac{\mathrm{d}^2}{\mathrm{d}y^2} + y^2\right] e^{-y^2/2} = | |||
\frac{1}{2}\left[e^{-y^2/2}\left(1 - y^2\right) + y^2 e^{-y^2/2}\right] = \frac{1}{2} e^{-y^2/2}. | |||
</math> | |||
We conclude that ψ<sub>0</sub>(''y'') ≡ exp(-''y''<sup>2</sup>/2) is an eigenfunction with eigenvalue | |||
:<math> | |||
\mathcal{E} = \frac{1}{2} \quad\Longrightarrow\quad E_0 = \tfrac{1}{2}\hbar \omega. | |||
</math> | |||
This encourages us to try a function of the form | |||
:<math> | |||
\psi(y) = e^{-y^2/2} f(y) = \psi_0(y) f(y). | |||
</math> | |||
Use the [[Leibniz formula]] | |||
:<math> | |||
\frac{d^2 (\psi_0 f)}{dy^2} = \frac{d^2 \psi_0} {dy^2}f + 2\frac{d \psi_0}{dy}\frac{df}{dy}+\frac{d^2 f} {dy^2}\psi_0 | |||
</math> | |||
and | |||
:<math> | |||
\frac{1}{2} \left[- \frac{d^2 \psi_0} {dy^2} + y^2 \psi_0\right] f = \frac{1}{2}\psi_0 f \quad | |||
\hbox{and} \quad \frac{d \psi_0}{dy} = - y\psi_0 | |||
</math> | |||
then we see | |||
:<math> | |||
\frac{1}{2}\left[- \frac{d^2 (\psi_0 f)}{dy^2} +y^2 \psi_0 f \right] = | |||
\frac{1}{2}\psi_0 f +y\psi_0\frac{df}{dy} - \frac{1}{2}\frac{d^2 f} {dy^2}\psi_0 = \mathcal{E} \psi_0 f. | |||
</math> | |||
Divide through by −ψ<sub>0</sub>(''y'')/2 and we find the equation for ''f'' | |||
:<math> | |||
\frac{d^2 f} {dy^2}-2y \frac{df}{dy} - f = -2\mathcal{E} f. | |||
</math> | |||
The differential equation of Hermite with [[Hermite polynomial|polynomial]] solutions ''H''<sub>''n''</sub>(''y'') is | |||
:<math> | |||
\frac{d^2 H_n}{dy^2}-2y\,\frac{dH_n}{dy}+ 2n H_n=0. | |||
</math> | |||
Due to the appearance of the integer coefficient 2''n'' in the last term the solutions are polynomials. We see that if we put | |||
:<math> | |||
2\mathcal{E} - 1 = 2n \quad \Longrightarrow \quad \mathcal{E} = n+\tfrac{1}{2}\quad \Longrightarrow\quad E = \hbar\omega (n+\tfrac{1}{2}) | |||
</math> | |||
that we have solved the Schrödinger equation for the harmonic oscillator. The unnormalized solutions are | |||
:<math> | |||
\psi(y) = e^{-y^2/2}\; H_n(y), \quad n = 0,1,2, \ldots | |||
</math> | |||
Revision as of 11:03, 30 January 2009
In quantum mechanics, the one-dimensional harmonic oscillator is one of the few systems that can be treated exactly. Its time-independent Schrödinger equation has the form
The two terms between square brackets are the Hamiltonian (energy operator) of the system: the first term is the kinetic energy operator and the second the potential energy operator. The quantity is Planck's reduced constant, m is the mass of the oscillator, and k is Hooke's spring constant. See the classical harmonic oscillator for further explanation of m and k.
The solutions of the Schrödinger equation are characterized by a vibration quantum number n = 0,1,2, .. and are of the form
Here
The functions Hn(x) are Hermite polynomials; the first few are:
The graphs of the first four eigenfunctions are shown in the figure. Note that the functions of even n are even, that is, , while those of odd n are antisymmetric
Solution of the Schrödinger equation
We rewrite the Schrödinger equation so as to hide the physical constants m, k, and h. As a first step we define the angular frequency ω ≡ √k/m, the same formula as for the classical harmonic oscillator:
Secondly, we divide through by , a factor that has dimension energy,
Write
and the Schrödinger equation becomes
Note that all constants are out of sight in the equation on the right.
A particular solution of this equation is
We verify this
so that
We conclude that ψ0(y) ≡ exp(-y2/2) is an eigenfunction with eigenvalue
This encourages us to try a function of the form
Use the Leibniz formula
and
then we see
Divide through by −ψ0(y)/2 and we find the equation for f
The differential equation of Hermite with polynomial solutions Hn(y) is
Due to the appearance of the integer coefficient 2n in the last term the solutions are polynomials. We see that if we put
that we have solved the Schrödinger equation for the harmonic oscillator. The unnormalized solutions are

![{\displaystyle \left[-{\frac {\hbar ^{2}}{2m}}{\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}+{\frac {1}{2}}kx^{2}\right]\psi =E\psi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d9f0668b35308e56ecebd650d35557a417587e9)






![{\displaystyle {\frac {1}{2}}\left[-{\frac {\hbar ^{2}}{m}}{\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}+m\omega ^{2}x^{2}\right]\psi =E\psi .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa364b4f4b0b31d74933d03ba31283324a200e95)

![{\displaystyle {\frac {1}{2}}\left[-{\frac {\hbar }{m\omega }}{\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}+{\frac {m\omega }{\hbar }}x^{2}\right]\psi ={\frac {E}{\hbar \omega }}\psi .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c52ece1d81ae4551f61d09b90fc3a758743f8ec)

![{\displaystyle {\frac {1}{2}}\left[-{\frac {1}{\beta ^{2}}}{\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}+\beta ^{2}x^{2}\right]\psi ={\mathcal {E}}\psi \quad \Longrightarrow \quad {\frac {1}{2}}\left[-{\frac {\mathrm {d} ^{2}}{\mathrm {d} y^{2}}}+y^{2}\right]\psi ={\mathcal {E}}\psi .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d1d15092a4e7bb074de00b75c4b9275b33c4e54)


![{\displaystyle {\frac {1}{2}}\left[-{\frac {\mathrm {d} ^{2}}{\mathrm {d} y^{2}}}+y^{2}\right]e^{-y^{2}/2}={\frac {1}{2}}\left[e^{-y^{2}/2}\left(1-y^{2}\right)+y^{2}e^{-y^{2}/2}\right]={\frac {1}{2}}e^{-y^{2}/2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93a7d91461e3cd6e73134967273d97d75c50c217)



![{\displaystyle {\frac {1}{2}}\left[-{\frac {d^{2}\psi _{0}}{dy^{2}}}+y^{2}\psi _{0}\right]f={\frac {1}{2}}\psi _{0}f\quad {\hbox{and}}\quad {\frac {d\psi _{0}}{dy}}=-y\psi _{0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf2e580c99c1105a568c3c229230f09a3d3960c9)
![{\displaystyle {\frac {1}{2}}\left[-{\frac {d^{2}(\psi _{0}f)}{dy^{2}}}+y^{2}\psi _{0}f\right]={\frac {1}{2}}\psi _{0}f+y\psi _{0}{\frac {df}{dy}}-{\frac {1}{2}}{\frac {d^{2}f}{dy^{2}}}\psi _{0}={\mathcal {E}}\psi _{0}f.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b28e76d23647ec69af861bee1b0a4c6d132f231)



