User:David MacQuigg/Sandbox/Shortest path routing

Figure 1. Computing the shortest path through a network

Figure 1. Computing the shortest path through a network

Figure 2. Time to build routing table using program here

Shortest path routing refers to the process of finding paths through a network that have a minimum of distance or other cost metric. Routing of data packets on the Internet is an example involving millions of routers in a complex, worldwide, multilevel network. Optimum routing on the Internet has a major impact on performance and cost.

This article will explain the basic routing algorithm that underlies the routing protocols used in real networks. A firm understanding of this algorithm will help in studying those protocols.

The algorithm is presented here in Python, a computer language designed for maximum readability. Computer networks texts often use pseudocode or C to explain algorithms. The problem with pseudocode is it can give you a temporary feeling of understanding, which is lost when you try to actually implement the algorithm, and stumble on the ambiguities you didn't notice, or find that real programs just don't work that way. The problem with C is that it is too low level. It's great for speed and efficiency, but you may get lost in the details of pointers and indices. You can follow every statement, and still not understand the algorithm. If you are not familiar with Python, see Dijkstra59.py for an annotated version of this program.

# dijkstra59v04.py           Dijkstra's Algorithm                   DMQ 12/16/09
'''
Use Dijkstra's algorithm to compute the shortest paths from a given
source node to all other nodes in a network. Links are bi-directional,
with the same distance in either direction.
'''
# Example from Figure 1 (8 nodes, 11 links)
nodeset = {'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H'}

linklist = [('A', 'B', 2), ('B', 'C', 7), ('C', 'D', 3), # (node,node,distance)
            ('B', 'E', 2), ('E', 'F', 2), ('F', 'C', 3),
            ('A', 'G', 6), ('G', 'E', 1), ('G', 'H', 4),
            ('F', 'H', 2), ('H', 'D', 2),               ]

INF = int(1e9)  # larger than any possible path
'''
The strategy is to start at the source node, send probes to each of its adjacent
nodes, pick the node with the shortest path from the source, and make that the
new working node.  Send probes from the new working node, pick the next shortest
path, and make that the next working node.  Continue selecting the shortest
possible path until every every node in the network has been selected.

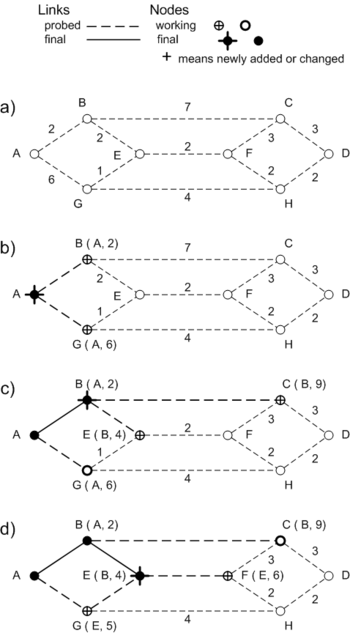
Figure 1 shows the first few steps in our example network. Labels on each node
show its distance from the source, and the previous node on the path from which
that distance was computed.  As new nodes are first probed, they are added to a
working set, shown with an open circle.  After each probe cycle, we look at the
entire set of working nodes.  The node with the shortest path is moved to a
final set, shown with a solid circle.  Figure 1b shows the situation after the
first probes from node 'A', with one node in the final set, and two nodes in the
working set.

The labels on nodes in the working set are tentative.  They will be replaced if
another probe arrives with a shorter total path.  Figure 1d shows node G getting
an update of its label after a probe from node E.  The updates at a node stop
when no other working set node has a shorter path.  This is the proof that the
method works.  The node with the shortest path in a working set can never get
any shorter, because subsequent probes can only come from other working nodes,
and those paths are already at least as long.

Figure 1i shows the final tree for node A.  The light dotted lines are links not
used in any shortest path from node A.  They might be used in another tree,
however.  Each node in a network can compute its own shortest path tree, given
the linklist for the entire network.
'''
def get_anodes(nodeset, linklist):
    '''Create a dictionary to quickly look up the adjacent nodes for any given
node.

>>> get_anodes(nodeset, linklist)
{'A': {('B', 2), ('G', 6)}, 'C': {('B', 7), ('F', 3), ('D', 3)}, \
'B': {('C', 7), ('E', 2), ('A', 2)}, 'E': {('B', 2), ('G', 1), ('F', 2)}, \
'D': {('H', 2), ('C', 3)}, 'G': {('A', 6), ('E', 1), ('H', 4)}, \
'F': {('H', 2), ('E', 2), ('C', 3)}, 'H': {('G', 4), ('D', 2), ('F', 2)}}

    '''
    anodes = {n:set() for n in nodeset} # start with empty set for each node
    for (n1, n2, x) in linklist:
        anodes[n1].add((n2, x))
        anodes[n2].add((n1, x))
        
    return anodes

def build_tree(src, anodes):
    '''Given a source node and a table of adjacent nodes for every node in a
network, return a table with two values for each node - the distance on the
shortest path from the source to that node, and the name of the next-to-last
node on that path.

A tree is more versatile than a routing table, because the last link along
every path is preserved, making it easy to reconstruct the path, as in Figure 1.
    
>>> build_tree('A', anodes)
{'A': ('A', 0), 'C': ('B', 9), 'B': ('A', 2), 'E': ('B', 4), \
'D': ('H', 10), 'G': ('E', 5), 'F': ('E', 6), 'H': ('F', 8)}
    '''
    # Current working node, and its distance from src
    wrk = src; dist = 0
    
    # Nodes in the working set and final set, saved as dictionaries.
    #   {key: value} = {nodename: label}
    #      label = (previous node along path, distance from src)
    Wset = {}; Fset = {}
    Fset[wrk] = (wrk, 0)  # starting node is always in Fset
    for (n, d) in anodes[wrk]:
        label = (wrk, d)
        Wset[n] = label

    while Wset:  # loop until the working set is empty
  
        # Find the shortest distance in the working set, and make that node the
        # new working node. The distance of that node will never get smaller.
        dist = INF
        for node in Wset:
            d = Wset[node][1]
            if d < dist:
                dist = d
                wrk = node

        # Move the new working node to the final set.        
        Fset[wrk] = Wset[wrk]
        del Wset[wrk]

        # Probe the nodes adjacent to wrk.      
        for (n, d) in anodes[wrk]:

            new_dist = dist + d
            
            if n in Fset:                # skip this node, already finalized
                continue
            
            elif (n in Wset) and (new_dist >= Wset[n][1]):
                continue                 # skip this probe, too long           

            else:  # Add new node to working set, or update existing node.
                Wset[n] = (wrk, new_dist)
    
    return Fset

def build_routing_table(src, anodes):
    '''Build a routing table directly from the anodes map.  The table has two
items for every destination node - the first step from src, and the total
distance along the shortest path.

>>> build_routing_table('A', anodes)
{'A': ('A', 0), 'C': ('B', 9), 'B': ('B', 2), 'E': ('B', 4), 'D': ('B', 10), \
'G': ('B', 5), 'F': ('B', 6), 'H': ('B', 8)}
    '''
    # Current working node, and its distance from src
    wrk = src; dist = 0
    
    # Nodes in the working set and final set, saved as dictionaries.
    #   {key: value} = {nodename: label}
    #      label = (first node along path, distance from src)
    Wset = {}; Fset = {}
    
    Fset[wrk] = (wrk, 0)  # starting node is always in Fset
    for (n, d) in anodes[wrk]:
        first = n             # first step on the new route
        Wset[n] = (first, d)  # label each new node in working set

    while Wset:  # loop until the working set is empty
         
        dist = INF
        for node in Wset:      # Find the shortest distance in the
            d = Wset[node][1]  # working set, and make that node the
            if d < dist:       # new working node. The distance of
                dist = d       # that node will never get smaller.
                wrk = node

        # Move the new working node to the final set.        
        Fset[wrk] = Wset[wrk]
        first = Wset[wrk][0]   # preserve the first step on the route.
        del Wset[wrk]

        # Probe the nodes adjacent to wrk. 
        for (n, d) in anodes[wrk]:

            new_dist = dist + d
            
            if n in Fset:                # skip this node, already finalized.
                continue
            
            elif (n in Wset) and (new_dist >= Wset[n][1]):
                continue                 # skip this probe, too long.           

            else:  # Add new node to working set, or update existing node.
                Wset[n] = (first, new_dist)
    
    return Fset

def get_path(dest, tree):
    '''Given destination node, and the dictionary returned by build_tree(),
return the shortest path from the top of the tree to dest.

>>> get_path('D', tree)
['A', 'B', 'E', 'F', 'H', 'D']
    '''
    wrk = dest  # Work backward from the destination node.
    prev = tree[wrk][0]  # previous node along path
    path = [wrk]
    
    while wrk != prev:      # top has no step back (wrk = prev)
        path.insert(0, prev)    # insert at beginning of list
        wrk = prev
        prev = tree[wrk][0]

    return path