Ellipse: Difference between revisions
imported>Paul Wormer |
imported>Paul Wormer |
||
| Line 120: | Line 120: | ||
</math> | </math> | ||
==Second degree equation== | |||
Under certain conditions the following equation of second degree in ''x'' and ''y'' represents an ellipse: | |||
:<math> | |||
f(x,y) \equiv Ax^2 +2Bxy + Cy^2 + 2Dx + 2Ey + F = 0. | |||
</math> | |||
In order to find the conditions we switch to matrix-vector notation and write the same expression as | |||
:<math> | |||
f(\mathbf{r}) = \mathbf{r}^\mathrm{T} \mathbb{A} \mathbf{r} + \mathbf{a}^\mathrm{T}\mathbf{r} +\mathbf{r}^\mathrm{T}\mathbf{a}+ F=0 | |||
</math> | |||
with | |||
:<math> | |||
\mathbf{r} \equiv \begin{pmatrix} x\\y\\ \end{pmatrix}, \quad | |||
\mathbb{A} \equiv \begin{pmatrix} A & B \\B & C\\ \end{pmatrix},\quad | |||
\mathbf{a} \equiv \begin{pmatrix} D\\E\\ \end{pmatrix}. | |||
</math> | |||
The superscript T stands for the transpose (row vector becomes column vector and vice versa). | |||
The expression can be rewritten by introducing the inverse of the matrix 𝔸. This gives the first condition: in order that the matrix be invertible its [[determinant]] det(𝔸) ≡ ''AC''−''B''<sup>2</sup> ≠ 0. | |||
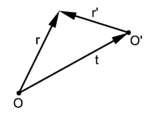
{{Image|Translation.png|right|150px|Fig. xxx. '''''r′''''' <nowiki>=</nowiki> '''''r''''' − '''''t'''''}} | |||
Then | |||
:<math> | |||
f(\mathbf{r}) =\left(\mathbf{r} + \mathbb{A}^{-1} \mathbf{a} \right)^\mathrm{T} \mathbb{A}\left(\mathbf{r} + \mathbb{A}^{-1} \mathbf{a} \right) - \mathbf{a}^\mathrm{T}\mathbb{A}^{-1}\mathbf{a} +F. | |||
</math> | |||
Define | |||
:<math> | |||
\mathbf{t} = - \mathbb{A}^{-1} \mathbf{a} \quad\Longrightarrow\quad | |||
\mathbb{A} \mathbf{t} = \mathbf{a}. | |||
</math> | |||
The minus sign in the definition of '''''t''''' is introduced to get the translation of the origin as depicted in figure xxx. Note that the vector '''''t''''' is easily obtained, namely by solving a set of two linear equations with '''''t''''' as right-hand side. | |||
Substitute '''''t''''' in the expression for ''f'': | |||
:<math> | |||
f(\mathbf{r}') = \left(\mathbf{r}'\right)^\mathrm{T} \mathbb{A} \mathbf{r}' + f(\mathbf{t}) | |||
\quad\hbox{with}\quad f(\mathbf{t}) = -\mathbf{a}^\mathrm{T}\mathbb{A}^{-1} \mathbf{a}+ F=0, | |||
</math> | |||
where we used | |||
:<math> | |||
\mathbb{A}^\mathrm{T} = \mathbb{A}\quad\Longrightarrow \quad \left(\mathbb{A}^{-1}\right) ^\mathrm{T} = \mathbb{A}^{-1}, | |||
</math> | |||
that is, the matrix 𝔸 and its inverse are symmetric. | |||
By translation of the origin over '''''t''''' the linear terms in ''f'' have been eliminated, only two quadratic terms, one bilinear term, and one constant term appear in | |||
:<math> | |||
f(\mathbf{r}') = \left(\mathbf{r}'\right)^\mathrm{T} \mathbb{A} \mathbf{r}' + f(\mathbf{t}). | |||
</math> | |||
The price paid for it is the requirement det(𝔸) ≠ 0. | |||
The next step is rotation of the ''x''′ and ''y''′ axis (with origin in O'), this will eliminate the bilinear term and decouple ''x''′ and ''y''′, the components of '''''r'''''′. | |||
==Polar representation relative to focus== | ==Polar representation relative to focus== | ||
{{Image|Ellipse3.png|right|300px|Fig. 4. Polar representation }} | {{Image|Ellipse3.png|right|300px|Fig. 4. Polar representation }} | ||
| Line 154: | Line 200: | ||
</math> | </math> | ||
and the polar equation for the ellipse follows. | and the polar equation for the ellipse follows. | ||
==Trammel construction== | ==Trammel construction== | ||
{{Image|Trammel.png|right|225px|Fig. 5. A trammel in theory}} | {{Image|Trammel.png|right|225px|Fig. 5. A trammel in theory}} | ||
Revision as of 07:30, 4 May 2010
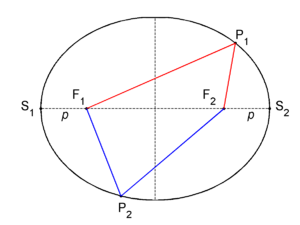
In mathematics, an ellipse is a planar locus of points characterized by having a constant sum of distances to two given fixed points in the plane. In figure 1 two fixed points F1 and F2 are shown, these are the foci of the ellipse. An arbitrary point P1 on the ellipse has distance F1P1 to F1 and distance F2P1 to F2. Let d be the sum of distances of P1 to the foci,
then all points of the ellipse have the constant sum of distances d. Thus, another arbitrary point P2 on the ellipse has distance F1P2 to F1 and distance F2P2 to F2. By definition the sum of distances of P2 to the foci is equal to d,
The horizontal line segment S1–S2 in figure 1, going through the foci, is known as the major axis of the ellipse.[1] Traditionally, the length of the major axis is indicated by 2a. The vertical dashed line segment, drawn halfway the foci perpendicular to the major axis, is referred to as the minor axis of the ellipse; its length is usually indicated by 2b. The major and minor axes are distinguished by a ≥ b.[2] When a = b the ellipse is a circle—a special case of an ellipse. The foci of a circle coincide with the center of the circle. Clearly both ellipse axes are symmetry axes, reflection in either of them transforms the ellipse into itself. Basically, this a consequence of the fact that reflection conserves (sums of) distances. The intersection of the axes is the center of the ellipse.
The two foci and the points S1 and S2 are connected by reflection in the minor axis. Hence the distance S2F2 ≡ p is by symmetry equal to the distance S1F1.[3] The distance of S2 to F1 is equal to 2a − p. By the definition of the ellipse the sum is equal to d, hence
The sum d of distances from any point on the ellipse to the foci is equal to the length of the major axis.
Conic section
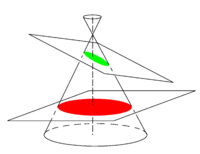
In the work of the Greek mathematician Apollonius (c. 262–190 BC) the ellipse arose as the intersection of a plane with a cone. Apollonius gave the ellipse its name, though the term ἐλλειψις (elleipsis, meaning "falling short") was used earlier by Euclid (c. 300 BC) in the construction of parallelograms with areas that "fell short". Apollonius applied the word to the conic section that at present we call ellipse. See Ref.[4] for the—in modern eyes—complicated reasoning by which Apollonius tied the shape of certain conic sections to Euclid's concept of deficient areas.
In figure 2 a cone with a circular base is shown. It has a vertical symmetry axis, an axis of revolution. A cone can be generated by revolving around the axis a line that intersects the symmetry axis under an angle. A horizontal intersecting plane (plane perpendicular to the symmetry axis of the cone) gives a circle (a special ellipse), that is, the intersection of a horizontal plane with the cone is a circle. Planes that make an angle less than, or equal to, 90° (but more than half the top angle of the cone) with the axis have an ellipse as intersection.
Eccentricity
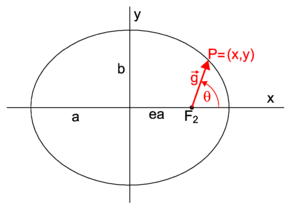
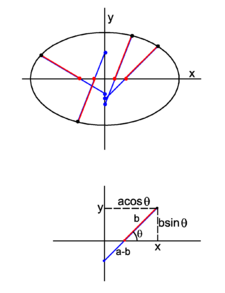
The eccentricity e of an ellipse (usually denoted by e or ε) is the ratio of the distance OF2 (cf. figure 3) to the length a (the semi-major axis), that is, e ≡ OF2 / a. Let be a vector of length a along the x-axis, then
The following two vectors have common endpoint at P, see figure 3,
Move P now to the positive y-axis; its new position vector is:
By symmetry, the distance of the moved P to either focus is equal to the semi-major axis a and equal to the length of the new vector (with endpoint on the y-axis). For the following two inner products (indicated by a centered dot) we find,
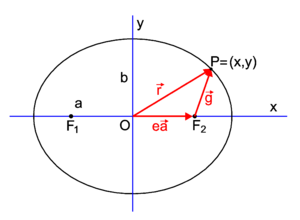
Fig. 3. An ellipse situated such that the major and minor axis are along Cartesian axes. The center of the ellipse coincides with the origin O.
Hence, (in fact by the Pythagoras theorem applicable for P on the y-axis),
so that the eccentricity is given by
Algebraic form
Consider an ellipse that is located with respect to a Cartesian frame as in figure 3 (major axis on x-axis, minor axis on y-axis). For a point P=(x,y) of the ellipse it holds that
Note that this equation is reminiscent of the equation for a unit circle. An ellipse may be seen as a unit circle in which the x and the y coordinates are scaled independently, by 1/a and 1/b, respectively.
Proof
Introduce the vectors
By definition of ellipse, the sum of the lengths is 2a
Multiply Eq. (1) by
and work out the left-hand side:
Hence
Use
and one obtains
Add and subtract Eqs (1) and (2) and we find expressions for the distance of P to the foci,
Square both equations
Adding, using the earlier derived value for e2, and reworking gives
Division by b2 gives finally
Second degree equation
Under certain conditions the following equation of second degree in x and y represents an ellipse:
In order to find the conditions we switch to matrix-vector notation and write the same expression as
with
The superscript T stands for the transpose (row vector becomes column vector and vice versa). The expression can be rewritten by introducing the inverse of the matrix 𝔸. This gives the first condition: in order that the matrix be invertible its determinant det(𝔸) ≡ AC−B2 ≠ 0.
Then
Define
The minus sign in the definition of t is introduced to get the translation of the origin as depicted in figure xxx. Note that the vector t is easily obtained, namely by solving a set of two linear equations with t as right-hand side. Substitute t in the expression for f:
where we used
that is, the matrix 𝔸 and its inverse are symmetric.
By translation of the origin over t the linear terms in f have been eliminated, only two quadratic terms, one bilinear term, and one constant term appear in
The price paid for it is the requirement det(𝔸) ≠ 0.
The next step is rotation of the x′ and y′ axis (with origin in O'), this will eliminate the bilinear term and decouple x′ and y′, the components of r′.
Polar representation relative to focus
The length g of the vector (cf. figure 4)
is given by the polar equation
where 2ℓ is known as the latus rectum (lit. right side) of the ellipse; it is equal to 2g for θ = 90° (twice the length of the vector when it makes a right angle with the major axis).
Proof
Earlier [Eq. (3)] it was derived for the distance from the right focus F2 to P that
Elimination of x from
gives
so that
Substitute
and the polar equation for the ellipse follows.
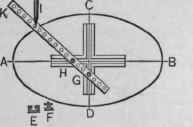
Trammel construction
Before drafting was done almost exclusively by the aid of computers, draftsmen used a simple device for drawing ellipses, a trammel. Basically, a trammel is a rigid bar of length a (semi-major axis). In the top drawing of figure 5 the bar is shown as a blue line segment bounded by a black and a blue bead. On this bar a segment of length b (semi-minor axis) is marked; this is the red segment on the bar. Two beads fixed to the rigid bar move back and forth along the x-axis and y-axis, respectively. The blue bead fixed at one end of the bar moves along the y-axis, the red bead, which marks the beginning of the red segment of length b, moves along the x-axis. The endpoint of the bar (the black bead in figure 5) moves along an ellipse with semi-major axis a and semi-minor axis b and typically has a pen fixed to it.
The fact that the trammel construction works is proved very easily, cf. the bottom drawing in figure 5,
Hence
which indeed is the equation for an ellipse.
A device called a trammel point is used to guide a woodworking router in making elliptical cuts.
Gardener's construction
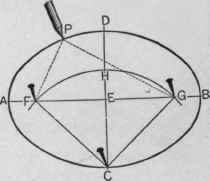
It is possible to construct an ellipse of given major and minor axis by the aid of a compass, a ruler, three thumbtacks, and a piece of string, see figure 7.
First draw the major axis AB, and then obtain with the compass its perpendicular bisector intersecting AB in the midpoint E. Along the bisector one measures off the length of the minor axis CD. Given that the distances CF and CG are the semi-major axis (AB/2), one can determine the foci by drawing an arc with the compass using C as center and AB/2 as radius. One now pins the thumbtacks in the foci and the point C and fixes a piece of string of length 2AB as shown in figure 7. Keeping the string taut one draws the upper part of the ellipse by moving the pencil from A to B. Then one removes the pin in point C and places it in D and repeats the procedure for the lower part of the ellipse.
Clearly this procedure can be used in the garden to create an elliptic lawn or flowerbed, which is why the procedure is sometimes referred to gardener's construction.
Notes
- ↑ The points S1 and S2 are the main vertices of the ellipse.
- ↑ The quantities a and b are referred to as semi-major and semi-minor axis, respectively. Note that, just as diameter of circle, semi-axis does not only refer to the line segment itself, but also to its length.
- ↑ The shortest distance of a focus to a point on the elllipse (= p) is the periapsis of the ellipse; the longest distance, S1F2=S2F1=2a−p, is the apoapsis.
- ↑ M. Kline, Mathematical Thought from Ancient to Modern Times, Oxford UP, New York (1972)
Figures 6 and 7 are from George Watson Kittredge, The New Metal Worker Pattern Book, David Williams Company, New York, (1901) Online