Area of a triangle: Difference between revisions
Jump to navigation
Jump to search

imported>Matt Mahlmann (added subpage template) |
imported>Gaurav Banga (heron's formula) |
||
| Line 1: | Line 1: | ||
{{subpages}} | {{subpages}} | ||
There are several ways to compute the area of a triangle. | |||
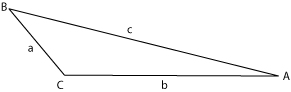
* <math> Area = \left(\frac{1}{2}\right)bc (sin A) = \left(\frac{1}{2}\right)ac (sin B) = \left(\frac{1}{2}\right)ab (sin C) </math> | |||
* <math> Area = \sqrt{ s (s-a) (s-b) (s-c)} </math> | |||
<math> Area = \left(\frac{1}{2}\right)bc (sin A) = \left(\frac{1}{2}\right)ac (sin B) = \left(\frac{1}{2}\right)ab (sin C) </math> | where <math> s = \frac{1}{2} (a+b+c) </math>is the [[semiperimeter]] of the triangle. This formula is known as the Heron's formula (or Hero's formula), named after the mathematician, [[Heron of Alexandria]]. | ||
[[Image:Triangle.jpg|center|frame|Triangle]] | [[Image:Triangle.jpg|center|frame|Triangle]] | ||
== Right triangles == | == Right triangles == | ||
Revision as of 08:16, 15 August 2008
There are several ways to compute the area of a triangle.
where is the semiperimeter of the triangle. This formula is known as the Heron's formula (or Hero's formula), named after the mathematician, Heron of Alexandria.
Right triangles
For right triangles, the angle C, opposite the hypotenuse (c), is 90 degrees. The sine of 90 degrees is 1, so the equation reduces to: