Golden ratio: Difference between revisions
imported>Malcolm Schosha (rm dictionary that is now redundant) |
imported>Daniel Mietchen m (why does it follow - see talk) |
||
| Line 3: | Line 3: | ||
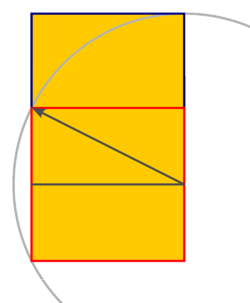
{{Image|1000px Golden Rectangle Construction.png|right|250px|demonstrating a simple method to construct a Golden Ratio rectangle}} | {{Image|1000px Golden Rectangle Construction.png|right|250px|demonstrating a simple method to construct a Golden Ratio rectangle}} | ||
{{Image|Altes Rathaus Leipzig.jpg|right|250px|The old [[townhall]] in [[Leipzig]]. The tower is positioned between the | {{Image|Altes Rathaus Leipzig.jpg|right|250px|The old [[townhall]] in [[Leipzig]]. The tower is positioned between the right (a) and left (b) sections so that <math>\scriptstyle \frac{a}{b}</math> equals the golden ratio.}} | ||
The '''golden ratio''' is a mathematical proportion that is important in the arts and interesting to mathematicians. In architecture and painting, some works have been proportioned to approximate the golden ratio ever since antiquity. It has been claimed that the golden ratio is found in the proportions of architectural structures ranging from the [[Great Pyramid of Giza]]<ref>[http://www.dartmouth.edu/~matc/math5.geometry/unit2/unit2.html]''The Golden Ratio & Squaring the Circle in the Great Pyramid'', Paul Calter</ref>, to the [[Parthenon]]<ref>[http://community.middlebury.edu/~harris/Humanities/TheGoldenMean.html] ''The Golden Mean'', William Harris</ref>, to [[Chartres Cathedral]]<ref>[http://www.johnjames.com.au/chartres-shorthistory.shtml] ''Chartres Cathedral'', John James</ref>. In the 20th century, the golden section was applied by the French architect [[Le Corbusier]]<ref>[http://www.archsociety.com/e107_plugins/content/content.php?content.24] ''Working With Corbusier'', Jerzy Soltan</ref>, who used the proportion in the design of virtually all his architectural works, and in his his painting, and who wrote a series of books on the subject called ''The Modulor''<ref>[http://books.google.com/books?id=5ja-3GavJssC&dq=The+Modulor&printsec=frontcover&source=bn&hl=en&ei=vcmnSr8akqo26ri5qwg&sa=X&oi=book_result&ct=result&resnum=8#v=onepage&q=&f=false] ''The Modulor'', vol.1, Le Corbusier</ref>. | The '''golden ratio''' is a mathematical proportion that is important in the arts and interesting to mathematicians. In architecture and painting, some works have been proportioned to approximate the golden ratio ever since antiquity. It has been claimed that the golden ratio is found in the proportions of architectural structures ranging from the [[Great Pyramid of Giza]]<ref>[http://www.dartmouth.edu/~matc/math5.geometry/unit2/unit2.html]''The Golden Ratio & Squaring the Circle in the Great Pyramid'', Paul Calter</ref>, to the [[Parthenon]]<ref>[http://community.middlebury.edu/~harris/Humanities/TheGoldenMean.html] ''The Golden Mean'', William Harris</ref>, to [[Chartres Cathedral]]<ref>[http://www.johnjames.com.au/chartres-shorthistory.shtml] ''Chartres Cathedral'', John James</ref>. In the 20th century, the golden section was applied by the French architect [[Le Corbusier]]<ref>[http://www.archsociety.com/e107_plugins/content/content.php?content.24] ''Working With Corbusier'', Jerzy Soltan</ref>, who used the proportion in the design of virtually all his architectural works, and in his his painting, and who wrote a series of books on the subject called ''The Modulor''<ref>[http://books.google.com/books?id=5ja-3GavJssC&dq=The+Modulor&printsec=frontcover&source=bn&hl=en&ei=vcmnSr8akqo26ri5qwg&sa=X&oi=book_result&ct=result&resnum=8#v=onepage&q=&f=false] ''The Modulor'', vol.1, Le Corbusier</ref>. | ||
| Line 9: | Line 9: | ||
The ratio itself is also known as the '''mean and extreme ratio''', the '''golden section''', the '''golden mean''', and the '''divine proportion'''. The earliest existing description is found in the [[Euclid's Elements|Elements]] of [[Euclid]] (Book 5, definition 3): ''A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the less.'' | The ratio itself is also known as the '''mean and extreme ratio''', the '''golden section''', the '''golden mean''', and the '''divine proportion'''. The earliest existing description is found in the [[Euclid's Elements|Elements]] of [[Euclid]] (Book 5, definition 3): ''A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the less.'' | ||
To be more elaborate: if there is a longer line segment <math>\scriptstyle a\ </math> and and a shorter line segment <math>\scriptstyle b\ </math>, and if the ratio between <math>\scriptstyle a + b\ </math> and <math>\scriptstyle a\ </math> is equal to the ratio between the line segment <math>\scriptstyle a\ </math> and <math>\scriptstyle b\ </math>, this ratio is the golden ratio | To be more elaborate: if there is a longer line segment <math>\scriptstyle a\ </math> and and a shorter line segment <math>\scriptstyle b\ </math>, and if the ratio between <math>\scriptstyle a + b\ </math> and <math>\scriptstyle a\ </math> is equal to the ratio between the line segment <math>\scriptstyle a\ </math> and <math>\scriptstyle b\ </math>, this ratio is the golden ratio <math>\scriptstyle \Phi = \frac{a}{b} = \frac{a+b}{a}</math>. | ||
==Properties== | ==Properties== | ||
Rewriting this definition gives | |||
:<math>\Phi = \frac{a}{b}= \frac{a+b}{a} = 1+\frac{b}{a} = 1+ \frac{1}{\Phi}</math>, | |||
which leads to | |||
:<math>\Phi^2-\Phi-1 = 0 </math>, | |||
a [[quadratic equation]] wit the solutions | |||
:<math>\Phi =\frac{1 + \sqrt{5}}{2} = 1 + \frac{1}{\Phi} = 1{,}618\,033\,988\dots</math> . | |||
and | |||
:<math>\bar \Phi=\frac{1 - \sqrt{5}}{2}= 1 - \Phi= -\frac{1}{\Phi} = -0{,}618\,033\,988\dots</math> | |||
With <math>\Phi = 1 + \frac{1}{\Phi}</math> we could derive the infinite [[continued fraction]] of the golden ratio: | With <math>\Phi = 1 + \frac{1}{\Phi}</math> we could derive the infinite [[continued fraction]] of the golden ratio: | ||
Revision as of 01:06, 10 September 2009
The golden ratio is a mathematical proportion that is important in the arts and interesting to mathematicians. In architecture and painting, some works have been proportioned to approximate the golden ratio ever since antiquity. It has been claimed that the golden ratio is found in the proportions of architectural structures ranging from the Great Pyramid of Giza[1], to the Parthenon[2], to Chartres Cathedral[3]. In the 20th century, the golden section was applied by the French architect Le Corbusier[4], who used the proportion in the design of virtually all his architectural works, and in his his painting, and who wrote a series of books on the subject called The Modulor[5].
The ratio itself is also known as the mean and extreme ratio, the golden section, the golden mean, and the divine proportion. The earliest existing description is found in the Elements of Euclid (Book 5, definition 3): A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the less.
To be more elaborate: if there is a longer line segment and and a shorter line segment , and if the ratio between and is equal to the ratio between the line segment and , this ratio is the golden ratio .
Properties
Rewriting this definition gives
- ,
which leads to
- ,
a quadratic equation wit the solutions
- .
and
With we could derive the infinite continued fraction of the golden ratio:
Thus
- ,
where is the n-th term of the Fibonacci sequence.