Area of a triangle: Difference between revisions
Jump to navigation
Jump to search

imported>Gaurav Banga (heron's formula) |
imported>James Yolkowski (mention most common formula) |
||
| Line 1: | Line 1: | ||
{{subpages}} | {{subpages}} | ||
There are several ways to compute the area of a triangle. | There are several ways to compute the area of a [[triangle]]. The most common formula is <math>Area = \frac{1}{2}bh</math>, where <math>b</math> is the ''base'', which can be any side, and <math>h</math> is the ''altitude'' of the triangle, which is the perpendicular distance from the base (or the line containing the base for obtuse triangles) to the corner opposite the base. This formula does require that the altitude be known; other formulae not having this requirement are: | ||
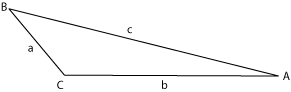
* <math> Area = \left(\frac{1}{2}\right)bc (sin A) = \left(\frac{1}{2}\right)ac (sin B) = \left(\frac{1}{2}\right)ab (sin C) </math> | * <math> Area = \left(\frac{1}{2}\right)bc (sin A) = \left(\frac{1}{2}\right)ac (sin B) = \left(\frac{1}{2}\right)ab (sin C) </math> | ||
Latest revision as of 21:18, 6 December 2009
There are several ways to compute the area of a triangle. The most common formula is , where is the base, which can be any side, and is the altitude of the triangle, which is the perpendicular distance from the base (or the line containing the base for obtuse triangles) to the corner opposite the base. This formula does require that the altitude be known; other formulae not having this requirement are:
where is the semiperimeter of the triangle. This formula is known as the Heron's formula (or Hero's formula), named after the mathematician, Heron of Alexandria.
Right triangles
For right triangles, the angle C, opposite the hypotenuse (c), is 90 degrees. The sine of 90 degrees is 1, so the equation reduces to: