Faraday's law (electromagnetism): Difference between revisions
imported>Paul Wormer No edit summary |
imported>Paul Wormer |
||
| Line 7: | Line 7: | ||
Faraday's law of electromagnetic induction relates the electromotive force<ref>The term EMF has historical origin, but is somewhat unfortunate as it is not a force but a potential.</ref> (EMF) <math>\scriptstyle \mathcal{E} </math> to the time derivative of the magnetic flux Φ. The law reads | Faraday's law of electromagnetic induction relates the electromotive force<ref>The term EMF has historical origin, but is somewhat unfortunate as it is not a force but a potential.</ref> (EMF) <math>\scriptstyle \mathcal{E} </math> to the time derivative of the magnetic flux Φ. The law reads | ||
:<math> | :<math> | ||
\mathcal{E} = - k \frac{d \Phi}{dt | \mathcal{E} = - k \frac{d \Phi}{dt} | ||
</math> | </math> | ||
where ''c'' | where ''k'' = 1 for [[SI]] units and one over ''c'' (the speed of light) for [[Gaussian unit]]s. | ||
The EMF is defined as | The EMF is defined as | ||
:<math> | :<math> | ||
\mathcal{E} \equiv \oint_C \mathbf{E}\cdot d\mathbf{l} , | \mathcal{E} \equiv \oint_C \mathbf{E}\cdot d\mathbf{l} , | ||
</math> | </math> | ||
where the electric field '''E''' is integrated around | where the electric field '''E''' is integrated around a closed path ''C''. | ||
The magnetic flux Φ through a surface ''S'' is defined as the surface integral | The magnetic flux Φ through a surface ''S'' that has ''C'' as boundary is defined as the surface integral, | ||
:<math> | :<math> | ||
\Phi \equiv \iint_{S} \mathbf{B}\cdot d\mathbf{S}, | \Phi \equiv \iint_{S} \mathbf{B}\cdot d\mathbf{S}, | ||
| Line 30: | Line 25: | ||
If, in the definition of the EMF, ''C'' is a conducting loop, then under influence of the EMF a current ''i''<sub>ind</sub> will run through it. The minus sign in Faraday's law has the consequence that the magnetic field generated by ''i''<sub>ind</sub> opposes the change in Φ; this phenomenon is known as [[Lenz' law]]. | If, in the definition of the EMF, ''C'' is a conducting loop, then under influence of the EMF a current ''i''<sub>ind</sub> will run through it. The minus sign in Faraday's law has the consequence that the magnetic field generated by ''i''<sub>ind</sub> opposes the change in Φ; this phenomenon is known as [[Lenz' law]]. | ||
If the surface ''S'' is constant in size and direction, a change in Φ is solely due to a change in '''B'''. | If the surface ''S'' is constant in size and direction, a change in Φ is solely due to a change in '''B'''. | ||
The magnetic flux can be varied by changing the angle between the field and surface. For the simple case of a planar loop bordering a constant area ''A'', and a homogeneous field '''B''' of strength ''B'', the flux is given by | |||
:<math> | :<math> | ||
\Phi(t) = A \mathbf{B}\cdot \hat{\mathbf{n}} = A B \cos\alpha(t), | \Phi(t) = A \mathbf{B}\cdot \hat{\mathbf{n}} = A B \cos\alpha(t) = \Phi(0)\cos\alpha(t), | ||
</math> | </math> | ||
where <math>\scriptstyle \hat{\mathbf{n}} </math> is a unit vector normal (perpendicular) to ''S''. Clearly, the flux is maximum if α = | |||
where <math>\scriptstyle \hat{\mathbf{n}} </math> is a unit vector normal (perpendicular) to the plane ''S'' bordered by the loop. The initial condition α(0) = 0° is applied. Clearly, the flux is maximum, Φ(0), if α = 0°, i.e., if '''B''' is perpendicular to ''S''. In the perpendicular case all of '''B''' passes through the surface. When '''B''' is parallel to surface, α = 90°, then there is no flux through the surface, Φ = 0, because '''B''' only grazes the surface. | |||
When α(t) becomes a function of time by rotation of the loop, Faraday's law shows that an EMF is induced, | |||
:<math> | |||
\mathcal{E} = k \Phi(0) \frac{d\alpha}{dt} \sin\alpha(t) . | |||
</math> | |||
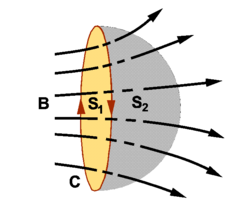
[[Image:Magnetic flux.png|right|thumb|250px|Magnetic flux. The flux through surface ''S''<sub>1</sub> (yellow) is equal to the flux through surface ''S''<sub>2</sub> (gray). Both surfaces have the contour ''C'' (red) as boundary.]] | [[Image:Magnetic flux.png|right|thumb|250px|Magnetic flux. The flux through surface ''S''<sub>1</sub> (yellow) is equal to the flux through surface ''S''<sub>2</sub> (gray). Both surfaces have the contour ''C'' (red) as boundary.]] | ||
The flux through two surfaces that together form a closed surface is equal because of [[Gauss' law (magnetism)|Gauss' law]]. Indeed, in the figure on the right the surfaces ''S''<sub>1</sub> and ''S''<sub>2</sub>, which have the boundary ''C'' in common, form together a closed surface. Hence Gauss' law states that | The flux through two surfaces that together form a closed surface is equal because of [[Gauss' law (magnetism)|Gauss' law]]. Indeed, in the figure on the right the surfaces ''S''<sub>1</sub> and ''S''<sub>2</sub>, which have the boundary ''C'' in common, form together a closed surface. Hence Gauss' law states that | ||
Revision as of 07:23, 5 July 2008
In electromagnetism, Faraday's law of electromagnetic induction states that a change in magnetic flux generates an electromotive force. The law is named after the English scientist Michael Faraday.
If one rotates a conducting loop in a static magnetic field, the magnetic flux through the surface of the loop is changed. This change induces an electromotive force (voltage difference) generating an electric current in the loop. Thus, the work done in rotating the loop inside a magnetic field is converted into an electric current. In other words, Faraday's law is the theoretical basis of the dynamo and the electric generator.
Mathematical formulation
Faraday's law of electromagnetic induction relates the electromotive force[1] (EMF) to the time derivative of the magnetic flux Φ. The law reads
where k = 1 for SI units and one over c (the speed of light) for Gaussian units. The EMF is defined as
where the electric field E is integrated around a closed path C. The magnetic flux Φ through a surface S that has C as boundary is defined as the surface integral,
where dS is a vector normal (perpendicular) to the infinitesimal surface element dS and dS is of length dS. The dot stands for the inner product between the magnetic induction B and dS.
In vacuum the magnetic induction B is proportional to the magnetic field H. (In SI units: B = μ0 H with μ0 the magnetic constant of the vacuum; in Gaussian units: B = H.)
If, in the definition of the EMF, C is a conducting loop, then under influence of the EMF a current iind will run through it. The minus sign in Faraday's law has the consequence that the magnetic field generated by iind opposes the change in Φ; this phenomenon is known as Lenz' law.
If the surface S is constant in size and direction, a change in Φ is solely due to a change in B.
The magnetic flux can be varied by changing the angle between the field and surface. For the simple case of a planar loop bordering a constant area A, and a homogeneous field B of strength B, the flux is given by
where is a unit vector normal (perpendicular) to the plane S bordered by the loop. The initial condition α(0) = 0° is applied. Clearly, the flux is maximum, Φ(0), if α = 0°, i.e., if B is perpendicular to S. In the perpendicular case all of B passes through the surface. When B is parallel to surface, α = 90°, then there is no flux through the surface, Φ = 0, because B only grazes the surface.
When α(t) becomes a function of time by rotation of the loop, Faraday's law shows that an EMF is induced,
The flux through two surfaces that together form a closed surface is equal because of Gauss' law. Indeed, in the figure on the right the surfaces S1 and S2, which have the boundary C in common, form together a closed surface. Hence Gauss' law states that
where the minus sign of the first term is due to the fact that the flux is into the volume enveloped by the two surfaces. It follows that
and that the magnetic flux Φ can be computed with respect to any surface that has C as boundary.
Connection to Maxwell's equation
Application of Stokes' theorem gives
where S is a surface that has C as boundary. From rewriting Faraday's law as follows,
and the fact that S is arbitrary, we may conclude
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{\nabla}\times \mathbf{E} = -k\frac{\partial\mathbf{B}}{\partial t}, }
which is one of Maxwell's equations. Recall that k = 1 for SI units and k = 1/c for Gaussian units.
Connection to Lorentz force
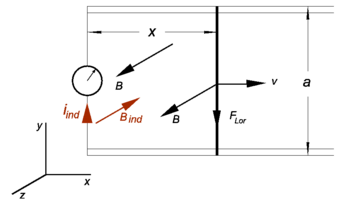
It is instructive to derive Faraday's law from the Lorentz force for a special case. To that end an experimental setup is depicted in the figure on the right. A conducting bar of length a moves in positive x direction over two parallel pairs of conducting rails. The speed v of the bar is constant. The whole setup is placed in a homogeneous magnetic field B = μ0 H (we are using SI units) that points toward the reader, i.e., in positive z-direction. Homogeneity means that everywhere in the plane of drawing a magnetic field B of the same strength points toward the reader (parallel to the z-axis).
The magnetic field is constant, but the surface S increases linearly in time
The vector B points in positive z-direction and so does the normal to S,
The time-dependence of the growing flux is solely due to the time-dependence of the growth of the surface. The time derivative of the magnetic flux in the figure is positive and equal to
The Lorentz force (in SI units) is the cross product,
where ey is a unit vector along the y-axis. In order to obtain the electromotive force (EMF) one must integrate the inner product of electric force with path, FLor⋅dl, counter-clockwise around the circuit consisting of: the moving bar, the two pairs of unmoving rails and the unmoving conductor containing the ampmeter. The integration is counter-clockwise because of the right-hand screw rule applied to the direction of B. Except for the moving bar, where the force is constant and non-zero, there is no force in the circuit. The constant force acts over the length a of the moving bar and gives an EMF equal to force times path length,
From equations (1) and (2) follows
which indeed is Faraday's law of magnetic induction.
The EMF gives a current iind in the direction of the Lorentz force, i.e., in a clockwise direction in the plane of drawing (the x-y plane). By Biot-Savart's law a current gives a circular magnetic field. The current iind has a tangent vector in the x-y plane that is in negative z-direction. Hence Bind opposes B, in accordance with Lenz' law.
Note
- ↑ The term EMF has historical origin, but is somewhat unfortunate as it is not a force but a potential.