User:David MacQuigg/Sandbox/Shortest path routing: Difference between revisions
Jump to navigation
Jump to search
imported>David MacQuigg No edit summary |
imported>David MacQuigg No edit summary |
||
| Line 1: | Line 1: | ||
{{Image|Shortest Path.png|center|350px|'''Figure 1. Computing the shortest path through a network'''}} | {{Image|Shortest Path.png|center|350px|'''Figure 1. Computing the shortest path through a network'''}} | ||
<pre> | <pre> | ||
# dijkstra59v03.py Shortest Path Routing DMQ 12/15/09 | # dijkstra59v03.py Shortest Path Routing DMQ 12/15/09 | ||
| Line 17: | Line 17: | ||
INF = int(1e9) # larger than any possible path | INF = int(1e9) # larger than any possible path | ||
''' | |||
The strategy is to start at the source node, send probes to each of its adjacent | |||
nodes, pick the node with the shortest path from the source, and make that the | |||
new working node. Send probes from the new working node, pick the next shortest | |||
path, and make that the next working node. Continue selecting the shortest | |||
possible path until every every node in the network has been selected. | |||
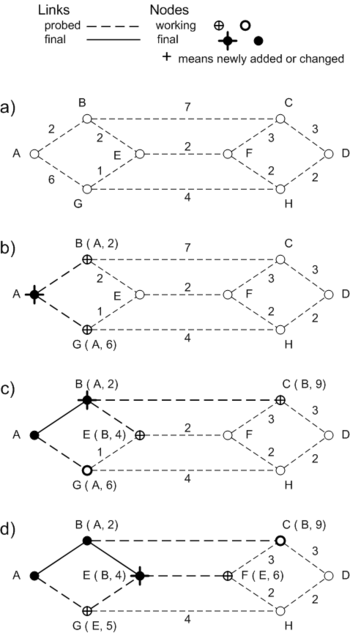
Figure 1 shows the first few steps in our example network. Labels on each node | |||
show its distance from the source, and the previous node on the path from which | |||
that distance was computed. As new nodes are first probed, they are added to a | |||
working set, shown with an open circle. After each probe cycle, we look at the | |||
entire set of working nodes. The node with the shortest path is moved to a | |||
final set, shown with a solid circle. Figure 1b shows the situation after the | |||
first probes from node 'A', with one node in the final set, and two nodes in the | |||
working set. | |||
The labels on nodes in the working set are tentative. They will be replaced if | |||
another probe arrives with a shorter total path. Figure 1d shows node G getting | |||
an update of its label after a probe from node E. The updates at a node stop | |||
when no other working set node has a shorter path. This is the proof that the | |||
method works. The node with the shortest path in a working set can never get | |||
any shorter, because subsequent probes can only come from other working nodes, | |||
and those paths are already at least as long. | |||
Figure 1i shows the final tree for node A. The light dotted lines are links not | |||
used in any shortest path from node A. They might be used in another tree, | |||
however. Each node in a network can compute its own shortest path tree, given | |||
the linklist for the entire network. | |||
''' | |||
def get_anodes(nodeset, linklist): | def get_anodes(nodeset, linklist): | ||
| Line 110: | Line 139: | ||
return path | return path | ||
</pre> | </pre> | ||
Revision as of 10:19, 16 December 2009
# dijkstra59v03.py Shortest Path Routing DMQ 12/15/09
'''
Use Dijkstra's algorithm to compute the shortest paths from a given
source node to all other nodes in a network. Links are bi-directional,
with the same distance in either direction.
'''
# Example from Figure 1 (8 nodes, 11 links)
nodeset = {'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H'}
linklist = [('A', 'B', 2), ('B', 'C', 7), ('C', 'D', 3), # (node,node,distance)
('B', 'E', 2), ('E', 'F', 2), ('F', 'C', 3),
('A', 'G', 6), ('G', 'E', 1), ('G', 'H', 4),
('F', 'H', 2), ('H', 'D', 2), ]
INF = int(1e9) # larger than any possible path
'''
The strategy is to start at the source node, send probes to each of its adjacent
nodes, pick the node with the shortest path from the source, and make that the
new working node. Send probes from the new working node, pick the next shortest
path, and make that the next working node. Continue selecting the shortest
possible path until every every node in the network has been selected.
Figure 1 shows the first few steps in our example network. Labels on each node
show its distance from the source, and the previous node on the path from which
that distance was computed. As new nodes are first probed, they are added to a
working set, shown with an open circle. After each probe cycle, we look at the
entire set of working nodes. The node with the shortest path is moved to a
final set, shown with a solid circle. Figure 1b shows the situation after the
first probes from node 'A', with one node in the final set, and two nodes in the
working set.
The labels on nodes in the working set are tentative. They will be replaced if
another probe arrives with a shorter total path. Figure 1d shows node G getting
an update of its label after a probe from node E. The updates at a node stop
when no other working set node has a shorter path. This is the proof that the
method works. The node with the shortest path in a working set can never get
any shorter, because subsequent probes can only come from other working nodes,
and those paths are already at least as long.
Figure 1i shows the final tree for node A. The light dotted lines are links not
used in any shortest path from node A. They might be used in another tree,
however. Each node in a network can compute its own shortest path tree, given
the linklist for the entire network.
'''
def get_anodes(nodeset, linklist):
'''Create a dictionary to quickly look up the adjacent nodes for any given
node.
>>> get_anodes(nodeset, linklist)
{'A': {('B', 2), ('G', 6)}, 'C': {('B', 7), ('F', 3), ('D', 3)}, \
'B': {('C', 7), ('E', 2), ('A', 2)}, 'E': {('B', 2), ('G', 1), ('F', 2)}, \
'D': {('H', 2), ('C', 3)}, 'G': {('A', 6), ('E', 1), ('H', 4)}, \
'F': {('H', 2), ('E', 2), ('C', 3)}, 'H': {('G', 4), ('D', 2), ('F', 2)}}
'''
anodes = {} # An empty dictionary to start
for n in nodeset:
lnks = set() # set of links to each node, initially none
for (n1, n2, x) in linklist: # scan for links connected to n
if n1 == n: lnks.add((n2, x))
if n2 == n: lnks.add((n1, x))
anodes[n] = lnks # all the links to node n
return anodes
def build_tree(src, anodes):
'''Given a source node and a table of adjacent nodes for every node in a
network, return a table with two values for each node - the distance on the
shortest path from the source to that node, and the name of the next-to-last
node on that path.
>>> build_tree('A', anodes)
{'A': ('A', 0), 'C': ('B', 9), 'B': ('A', 2), 'E': ('B', 4), \
'D': ('H', 10), 'G': ('E', 5), 'F': ('E', 6), 'H': ('F', 8)}
'''
# Current working node, and its distance from src
wrk = src; dist = 0
# Nodes in the working set and final set, saved as dictionaries.
# {key: value} = {nodename: label}
# label = (previous node along path, distance from src)
Wset = {}; Fset = {}
Fset[wrk] = (wrk, 0) # starting node is always in Fset
for (n, d) in anodes[wrk]:
label = (wrk, d)
Wset[n] = label
while Wset: # loop until the working set is empty
# Find the shortest distance in the working set, and make that node the
# new working node. The distance of that node will never get smaller.
dist = INF
for node in Wset:
d = Wset[node][1]
if d < dist:
dist = d
wrk = node
# Move the new working node to the final set.
Fset[wrk] = Wset[wrk]
del Wset[wrk]
# Probe the nodes adjacent to wrk.
for (n, d) in anodes[wrk]:
new_dist = dist + d
if n in Fset: # skip this node, already finalized
continue
elif (n in Wset) and (new_dist >= Wset[n][1]):
continue # skip this probe, too long
else: # Add new node to working set, or update existing node.
Wset[n] = (wrk, new_dist)
return Fset
def get_path(src, dest, tree):
'''Given source and destination nodes, and the dictionary returned by
build_tree(), return the shortest path through the network.
>>> get_path('A', 'D', tree)
['A', 'B', 'E', 'F', 'H', 'D']
'''
wrk = dest # Work backward from the destination node.
path = []
while wrk != src:
path.append(wrk)
wrk = tree[wrk][0] # step back to previous node
path.append(src) # don't forget to include the source
path.reverse()
return path