Revision as of 05:52, 23 January 2008 by imported>Paul Wormer
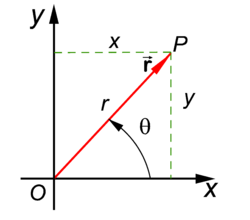
Two dimensional polar coordinates
r and θ of vector

In mathematics and physics, polar coordinates give the position of a vector  in two-dimensional real space
in two-dimensional real space  . A Cartesian system of two orthogonal axes is presupposed. One number (r) gives the length of the vector and the other number (θ) gives the angle of the vector with the x-axis of the Cartesian system (measured in the direction of the positive y-axis).
. A Cartesian system of two orthogonal axes is presupposed. One number (r) gives the length of the vector and the other number (θ) gives the angle of the vector with the x-axis of the Cartesian system (measured in the direction of the positive y-axis).
Definition
The polar coordinates are related to the Cartesian coordinates x and y through

so that for r ≠ 0,





