Revision as of 11:03, 30 January 2009 by imported>Paul Wormer
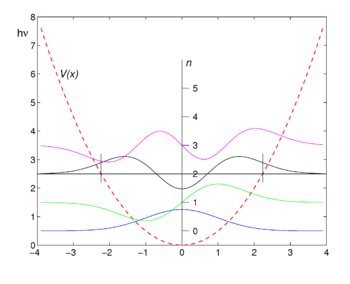
First four harmonic oscillator functions ψ
n. Potential
V(
x) is shown as reference. Function values are shifted upward by the corresponding energy values

In quantum mechanics, the one-dimensional harmonic oscillator is one of the few systems that can be treated exactly. Its time-independent Schrödinger equation has the form
![{\displaystyle \left[-{\frac {\hbar ^{2}}{2m}}{\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}+{\frac {1}{2}}kx^{2}\right]\psi =E\psi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d9f0668b35308e56ecebd650d35557a417587e9)
The two terms between square brackets are the Hamiltonian (energy operator) of the system: the first term is the kinetic energy operator and the second the potential energy operator.
The quantity  is Planck's reduced constant, m is the mass of the oscillator, and k is Hooke's spring constant. See the classical harmonic oscillator for further explanation of m and k.
is Planck's reduced constant, m is the mass of the oscillator, and k is Hooke's spring constant. See the classical harmonic oscillator for further explanation of m and k.
The solutions of the Schrödinger equation are characterized by a vibration quantum number n = 0,1,2, .. and are of the form

Here

The functions Hn(x) are Hermite polynomials; the first few are:

The graphs of the first four eigenfunctions are shown in the figure. Note that the functions of even n are even, that is,  , while those of odd n are antisymmetric
, while those of odd n are antisymmetric 
Solution of the Schrödinger equation
We rewrite the Schrödinger equation so as to hide the physical constants m, k, and h. As a first step we define the angular frequency ω ≡ √k/m, the same formula as for the classical harmonic oscillator:
![{\displaystyle {\frac {1}{2}}\left[-{\frac {\hbar ^{2}}{m}}{\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}+m\omega ^{2}x^{2}\right]\psi =E\psi .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa364b4f4b0b31d74933d03ba31283324a200e95)
Secondly, we divide through by  , a factor that has dimension energy,
, a factor that has dimension energy,
![{\displaystyle {\frac {1}{2}}\left[-{\frac {\hbar }{m\omega }}{\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}+{\frac {m\omega }{\hbar }}x^{2}\right]\psi ={\frac {E}{\hbar \omega }}\psi .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c52ece1d81ae4551f61d09b90fc3a758743f8ec)
Write

and the Schrödinger equation becomes
![{\displaystyle {\frac {1}{2}}\left[-{\frac {1}{\beta ^{2}}}{\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}+\beta ^{2}x^{2}\right]\psi ={\mathcal {E}}\psi \quad \Longrightarrow \quad {\frac {1}{2}}\left[-{\frac {\mathrm {d} ^{2}}{\mathrm {d} y^{2}}}+y^{2}\right]\psi ={\mathcal {E}}\psi .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d1d15092a4e7bb074de00b75c4b9275b33c4e54)
Note that all constants are out of sight in the equation on the right.
A particular solution of this equation is

We verify this

so that
![{\displaystyle {\frac {1}{2}}\left[-{\frac {\mathrm {d} ^{2}}{\mathrm {d} y^{2}}}+y^{2}\right]e^{-y^{2}/2}={\frac {1}{2}}\left[e^{-y^{2}/2}\left(1-y^{2}\right)+y^{2}e^{-y^{2}/2}\right]={\frac {1}{2}}e^{-y^{2}/2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93a7d91461e3cd6e73134967273d97d75c50c217)
We conclude that ψ0(y) ≡ exp(-y2/2) is an eigenfunction with eigenvalue

This encourages us to try a function of the form

Use the Leibniz formula

and
![{\displaystyle {\frac {1}{2}}\left[-{\frac {d^{2}\psi _{0}}{dy^{2}}}+y^{2}\psi _{0}\right]f={\frac {1}{2}}\psi _{0}f\quad {\hbox{and}}\quad {\frac {d\psi _{0}}{dy}}=-y\psi _{0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf2e580c99c1105a568c3c229230f09a3d3960c9)
then we see
![{\displaystyle {\frac {1}{2}}\left[-{\frac {d^{2}(\psi _{0}f)}{dy^{2}}}+y^{2}\psi _{0}f\right]={\frac {1}{2}}\psi _{0}f+y\psi _{0}{\frac {df}{dy}}-{\frac {1}{2}}{\frac {d^{2}f}{dy^{2}}}\psi _{0}={\mathcal {E}}\psi _{0}f.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b28e76d23647ec69af861bee1b0a4c6d132f231)
Divide through by −ψ0(y)/2 and we find the equation for f

The differential equation of Hermite with polynomial solutions Hn(y) is

Due to the appearance of the integer coefficient 2n in the last term the solutions are polynomials. We see that if we put

that we have solved the Schrödinger equation for the harmonic oscillator. The unnormalized solutions are



![{\displaystyle \left[-{\frac {\hbar ^{2}}{2m}}{\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}+{\frac {1}{2}}kx^{2}\right]\psi =E\psi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d9f0668b35308e56ecebd650d35557a417587e9)






![{\displaystyle {\frac {1}{2}}\left[-{\frac {\hbar ^{2}}{m}}{\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}+m\omega ^{2}x^{2}\right]\psi =E\psi .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa364b4f4b0b31d74933d03ba31283324a200e95)

![{\displaystyle {\frac {1}{2}}\left[-{\frac {\hbar }{m\omega }}{\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}+{\frac {m\omega }{\hbar }}x^{2}\right]\psi ={\frac {E}{\hbar \omega }}\psi .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c52ece1d81ae4551f61d09b90fc3a758743f8ec)

![{\displaystyle {\frac {1}{2}}\left[-{\frac {1}{\beta ^{2}}}{\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}+\beta ^{2}x^{2}\right]\psi ={\mathcal {E}}\psi \quad \Longrightarrow \quad {\frac {1}{2}}\left[-{\frac {\mathrm {d} ^{2}}{\mathrm {d} y^{2}}}+y^{2}\right]\psi ={\mathcal {E}}\psi .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d1d15092a4e7bb074de00b75c4b9275b33c4e54)


![{\displaystyle {\frac {1}{2}}\left[-{\frac {\mathrm {d} ^{2}}{\mathrm {d} y^{2}}}+y^{2}\right]e^{-y^{2}/2}={\frac {1}{2}}\left[e^{-y^{2}/2}\left(1-y^{2}\right)+y^{2}e^{-y^{2}/2}\right]={\frac {1}{2}}e^{-y^{2}/2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93a7d91461e3cd6e73134967273d97d75c50c217)



![{\displaystyle {\frac {1}{2}}\left[-{\frac {d^{2}\psi _{0}}{dy^{2}}}+y^{2}\psi _{0}\right]f={\frac {1}{2}}\psi _{0}f\quad {\hbox{and}}\quad {\frac {d\psi _{0}}{dy}}=-y\psi _{0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf2e580c99c1105a568c3c229230f09a3d3960c9)
![{\displaystyle {\frac {1}{2}}\left[-{\frac {d^{2}(\psi _{0}f)}{dy^{2}}}+y^{2}\psi _{0}f\right]={\frac {1}{2}}\psi _{0}f+y\psi _{0}{\frac {df}{dy}}-{\frac {1}{2}}{\frac {d^{2}f}{dy^{2}}}\psi _{0}={\mathcal {E}}\psi _{0}f.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b28e76d23647ec69af861bee1b0a4c6d132f231)



