Electron orbital

In quantum chemistry, an electron orbital (or more often just orbital) is a synonym for a one-electron function. Here "orbital" is used as a noun. In quantum mechanics, the adjective orbital is often used as a synonym of "spatial" (as in orbital angular momentum), in contrast to spin (as in spin angular momentum).

The majority of quantum chemical methods expect that an orbital has a finite norm, i.e., that the orbital is normalizable (quadratically integrable), and hence this requirement is often added to the definition.

Outside of quantum chemistry an orbital is often seen as a wave function. This point of view is a narrowing of the quantum chemical definition, but not contradictory to it, provided a wave function is seen in this context as a solution of an (effective) one-electron Schrödinger equation. Indeed, in the past quantum chemists, too, distinguished one-electron functions from orbitals, the former being fairly arbitrary and the latter being solutions of certain one-electron Schrödinger equations. This distinction faded away from quantum chemistry, leading to the present definition as "normalizable one-electron function."

Usually on distinguishes two kinds of orbitals: atomic orbitals and molecular orbitals. Atomic orbitals are expressed with respect to one Cartesian system of axes centered on a single atom. Molecular orbitals (MOs) are "spread out" over a molecule. Usually this is a consequence of an MO being a linear combination (weighted sum) of atomic orbitals centered on different atoms.

Definitions of orbitals

Several kinds of orbitals can be distinguished.

Atomic orbital

The basic kind of orbital is the atomic orbital (AO). This is a function depending on a single 3-dimensional vector r_A1, which is a vector pointing from point A to electron 1. Generally there is a nucleus at A. The following notations for an AO are frequently used,

$\chi _{i}(\mathbf {r} _{A1}),\quad {\hbox{or}}\quad \chi _{Ai}(\mathbf {r} _{1})$

but other notations can be found in the literature. In the second notation the center A is added as an index to the orbital. We say that χ_{A i} (or, as the case may be, χ _i) is centered at A. In numerical computations AOs are either taken as Slater type orbitals (STOs) or Gaussian type orbitals (GTOs). Hydrogen-like orbitals are rarely applied in numerical calculations, because they are not complete and fairly difficult to handle.

The orbital is quadratically integrable, which means that the following integral is finite,

$0\leq \int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\chi _{i}(\mathbf {r} _{A1})^{*}\chi _{i}(\mathbf {r} _{A1})\;dx_{A1}\,dy_{A1}\,dz_{A1}\ <\infty .$

Its integrand being real and non-negative, the integral is real and non-negative. The integral is zero if and only if χ _i is the zero function.

Molecular orbital

The second kind of orbital is the molecular orbital (MO). Such a one-electron function depends on several vectors: r_A1, r_B1, r_C1, ... where A, B, C, ... are different points in space (usually nuclear positions). The oldest example of an MO (without use of the name MO yet) is in the work of Burrau (1927) on the single-electron ion H₂⁺. Burrau applied spheroidal coordinates (a bipolar coordinate system) to describe the wave functions of the electron of H₂⁺.

Lennard-Jones introduced the following linear combination of atomic orbitals (LCAO) way of writing an MO φ:

$\phi (\mathbf {r} _{1})=\sum _{A=1}^{N_{\mathrm {nuc} }}\sum _{i=1}^{n_{A}}c_{Ai}\chi _{i}(\mathbf {r} _{A1}),\qquad c_{Ai}\in \mathbb {C} ,$

where A runs over N_nuc different points in space (usually A runs over all the nuclei of a molecule, hence the name molecular orbital), and i runs over the n_A different AOs centered at A. The complex coefficients c _Ai can be calculated by any of the existing effective-one-electron quantum chemical methods. Examples of such methods are the Hückel method and the Hartree-Fock method.

Spinorbitals

The AOs and MOs defined so far depend only on the spatial coordinate vector r_A1 of electron 1. In addition, an electron has a spin coordinate μ, which can have two values: spin-up or spin-down. A complete set of functions of μ consists of two functions only, traditionally these are denoted by α(μ) and β(μ). These functions are eigenfunctions of the z-component s_z of the spin angular momentum operator with eigenvalues ±½.

Spin atomic orbital

The most general spin atomic orbital of electron 1 is of the form

$\chi _{i}^{+}(\mathbf {r} _{A1})\alpha (\mu _{1})+\chi _{i}^{-}(\mathbf {r} _{A1})\beta (\mu _{1})$

which in general is not an eigenfunction of s_z. More common is the use of either

$\chi _{i}(\mathbf {r} _{A1})\alpha (\mu _{1})\quad {\hbox{or}}\quad \chi _{i}(\mathbf {r} _{A1})\beta (\mu _{1}),$

which are eigenfunctions of s_z. Since it is rare that different AOs are used for spin-up and spin-down electrons, we dropped the superscripts + and −.

Spin molecular orbital

A spin molecular orbital is usually either

$\phi ^{+}(\mathbf {r} _{1})\alpha (\mu _{1})\quad {\hbox{or}}\quad \phi ^{-}(\mathbf {r} _{1})\beta (\mu _{1}).$

Here the superscripts + and − might be necessary, because some quantum chemical methods distinguish the spatial wave functions of electrons with different spins. These are the so-called different orbitals for different spins (DODS) (or spin-unrestricted) methods. However, many quantum chemical methods apply the spin-restriction:

$\phi ^{+}(\mathbf {r} _{1})=\phi ^{-}(\mathbf {r} _{1})=\phi (\mathbf {r} _{1}).$

Chemists express this spin-restriction by stating that two electrons [electron 1 with spin up (α), and electron 2 with spin down (β)] are placed in the same spatial orbital φ. This means that the total N-electron wave function contains a factor of the type φ(r₁)α(μ₁)φ(r₂)β(μ₂).

History of term

Orbit is an old noun introduced by Johannes Kepler in 1609 to describe the paths of the earth and the planets. The adjective "orbital" had (and still has) the meaning "relating to an orbit". When Ernest Rutherford in 1911 postulated his planetary model of the atom (the nucleus as the Sun, and the electrons as the planets) it was natural to call the paths of the electrons "orbits". Bohr, although he was the first to recognize (1913) orbits as stationary states of the hydrogen atom, used the word as well. However, after Schrödinger (1926) had solved his wave equation for the hydrogen atom (see this article for details), it became clear that the electronic "orbits" did not resemble planetary orbits at all. The wave functions of the hydrogen electron are time-independent and smeared out. They are more like unmoving clouds than like planetary orbits. As a matter of fact, the angular parts of the hydrogen wave functions are spherical harmonics and hence they have the same appearance as spherical harmonics. (See spherical harmonics for a few graphical illustrations).

In the 1920s electron spin was discovered, whereupon the adjective "orbital" started to be used in the meaning of "non-spin", that is, as a synonym of "spatial". In scientific papers of around 1930 one finds discussions about "orbital degeneracy", meaning that the spatial (non-spin) parts of several one-electron wave functions have the same energy. Also the terms orbital- and spin-angular momentum date form these days.

In 1932 Robert S. Mulliken coined the noun "orbital". He wrote: From here on, one-electron orbital wave functions will be referred to for brevity as orbitals. Then he went on to distinguish atomic and molecular orbitals.

Later the somewhat unfortunate term "spinorbital" was introduced for the product functions φ(r₁)α(μ₁) and φ(r₁)β(μ₁) in which φ(r₁) has the tautological name "spatial orbital" and α(μ₁) and β(μ₁) are called "one-electron spin functions". The term "spinorbital" is unfortunate because it merges in one word the concepts of spin and orbital, which were distinguished carefully by early writers on quantum mechanics. For instance, one of the pioneers of theoretical chemistry, Walter Heitler, juxtaposes two-electron spin functions and two-electron orbital functions. In the phrase "two-electron orbital function", Heitler uses orbital as an adjective synonymous with spatial (non-spin). Note, parenthetically, that Heitler does not refer to a "two-electron orbital", (there is no such thing as a two-electron orbital!). However, an inexperienced reader may easily and erroneously interpret the term "two-electron orbital function" as "two-electron orbital".

Applications

Before the advent of electronic computers, orbitals (molecular as well as atomic) were used extensively in qualitative arguments explaining several properties of atoms and molecules. Orbitals still play this role in introductory texts and also in organic chemistry, where orbitals serve in the explanation of some reaction mechanisms, for instance in the Woodward-Hoffmann rules. In modern computational quantum chemistry the role of atomic orbitals is different; they serve as a convenient expansion basis, comparable to powers of x in a Taylor expansion of a function f(x), or sines and cosines in a Fourier series. Below, the role of atomic and molecular orbitals in qualitative theories will be discussed. The final subsection is devoted to the use of AOs in modern quantum chemistry.

Atomic orbitals

Bohr was the first to see how atomic orbitals form a basis for an understanding of the Periodic Table of elements. In Bohr's explanation of the Periodic Table, the atomic orbitals carry the same labels as hydrogen orbitals. That is, they have a principal quantum number n and a letter (s, p,...) designating the azimuthal quantum number (angular momentum quantum number) l.

The quantum numbers n and l are also valid labels for AOs that arise as solutions from an N-electron independent-particle model with a central (spherically symmetric) potential field. The central field approximation, which entails the spherical averaging of the field due to the electrons, is necessary to have l as a good quantum number. An independent-particle model leads to an effective-one-electron Schrödinger equation—one electron in the averaged (mean) field of the other electrons. The solutions of a mean field equation are orbitals and orbital-energies. So, orbitals and orbital-energies do not only arise in real one-electron systems, such as the H-atom, but also in independent-particle approximations of N-electron systems.

Two major differences between an atomic effective-one-electron model and the hydrogen-like atom are:

1. The radial solutions are given numerically, and are no longer known analytic functions, such as the Laguerre functions for the hydrogen-like atom. The angular parts, however, are the same analytic functions (spherical harmonics) as in the case of the hydrogen-like-atom.
2. The high degeneracy of the H-atom is lifted. In the hydrogen atom all orbitals of certain n are degenerate. For instance, the orbitals in the n = 4 shell: 4s, 4p, 4d, and 4f, all have the same energy (proportional to 1/n² = 1/16). In the N-electron atom only the AOs of the same azimuthal quantum number l are degenerate.

Note the role of the principal quantum number n in the effective-one-electron model. It is simply an index that counts increasing orbital energies, starting at n = l + 1 (to be in line with the hydrogen-like AOs). In summary, an atomic orbital of an N-electron atom is labeled by n (indicating its energy) and l (indicating its angular momentum).

It is found that the orbitals arising from the central field, independent-particle model applied to different atoms have the following order in increasing energy

1s, 2s, 2p, 3s, 3p, 3d, 4s, 4p, 4d, 5s, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d.

For some atoms the order of 3d and 4s is flipped and for some other atoms the order of 4d and 5s is flipped. Note further that, for example 4f is not degenerate with 4d, which is the case for hydrogen-like atoms.

Knowing this order, one can build up the atoms in the Periodic Table by the Aufbau (building-up) principle: fill orbitals in increasing energy. Doing this one must obey the Pauli exclusion principle that forbids more than two electrons per spatial orbital. Allowed is at most one electron with α spin and one with β spin. In addition recall that there are 2l+1 orbitals of certain l. For instance, the neon atom (atomic number Z = 10) has the electronic configuration (n = 1 and n = 2 shells are completely filled):

${\scriptstyle 1s^{2}\,2s^{2}\,2p^{6},}$

meaning two electrons are in the 1s, two electrons in the 2s, and six electrons in the 2p AOs. Similarly, chlorine (Z = 17) has

${\scriptstyle 1s^{2}\,2s^{2}\,2p^{6}\,3s^{2}\,3p^{5}\,}.$

For more details the article Periodic Table may be consulted. A list of the electronic configurations of the ground states of the first 94 elements may be found here.

Molecular orbitals

In the hands of Friedrich Hund, Robert S. Mulliken, John Lennard-Jones, and others, molecular orbital theory was established firmly in the 1930s as a (mostly qualitative) theory explaining much of chemical bonding, especially the bonding in diatomic molecules.

MO energy level diagram for H₂

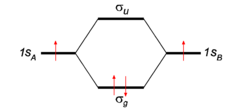
To give the flavor of the theory we look at the simplest molecule: H₂. The two hydrogen atoms, labeled A and B, each have one electron (a red arrow in the figure) in an 1s atomic orbital (AO). These AOs are labeled in the figure 1s_A and 1s_B. When the atoms start to interact the AOs combine linearly to two molecular orbitals:

$\sigma _{g}=N_{g}(1s_{A}+1s_{B})\quad {\hbox{and}}\quad \sigma _{u}=N_{u}(1s_{A}-1s_{B}).$

Earlier in this article a general expression for an LCAO-MO was given. In the present example of the σ_g MO of H₂, we have N_nuc = 2, n_A = n_B = 1, χ_A1 = 1s_A, χ_B1 = 1s_B, c_A1 = c_B1 = N_g. With regard to the form of the MOs the following: Because both hydrogen atoms are identical, the molecule has reflection symmetry with respect to a mirror plane halfway the H—H bond and perpendicular to it. It is one of the basic assumptions in quantum mechanics that wave functions show the symmetry of the system. [Technically: solutions of the Schrödinger equation belong to a subspace of Hilbert (function) space that is irreducible under the symmetry group of the system]. Clearly σ_g is symmetric (is even, stays the same) under

$\mathrm {\scriptstyle Reflection:} \quad 1s_{A}\longleftrightarrow 1s_{B},$

while σ_u changes sign (is antisymmetric, is odd). The Greek letter σ indicates invariance under rotation around the bond axis. The subscripts g and u stand for the German words gerade (even) and ungerade (odd). So, because of the high symmetry of the molecule we can immediately write down two molecular orbitals, which evidently are linear combinations of atomic orbitals.

The normalization factors N_g and N_u and the orbital energies are still to be computed. The normalization constants follow from requiring the MOs to be normalized to unity. In the computation we will use the bra-ket notation for the integral over x_A1, y_A1, and z_A1 (or over x_B1, y_B1, and z_B1 when that is easier).

$1=\langle \sigma _{g}|\sigma _{g}\rangle =N_{g}^{2}\left(\langle 1s_{A}|1s_{A}\rangle +\langle 1s_{B}|1s_{B}\rangle +\langle 1s_{A}|1s_{B}\rangle +\langle 1s_{B}|1s_{A}\rangle \right)=N_{g}^{2}(2+2S).$

We used here that the AOs are normalized to unity and that the overlap integral is real

$\langle 1s_{A}|1s_{B}\rangle =\langle 1s_{B}|1s_{A}\rangle \equiv S.$

Applying the same procedure for N_u, we find for the two normalization factors

$N_{g}=\left[2+2S\right]^{-1/2}\quad {\hbox{and}}\quad N_{u}=\left[2-2S\right]^{-1/2}.$

At this point one often assumes that S ≅ 0, so that both normalization factors are equal to ½√2.

In order to calculate the energy of an orbital we introduce an effective-one-electron energy operator (Hamiltonian) h,

${\begin{aligned}E_{\sigma _{g}}&=\langle \sigma _{g}|h|\sigma _{g}\rangle \\&={\frac {1}{2}}\left(\langle 1s_{A}|h|1s_{A}\rangle +\langle 1s_{B}|h|1s_{B}\rangle +\langle 1s_{A}|h|1s_{B}\rangle +\langle 1s_{B}|h|1s_{A}\rangle \right)\\&\equiv {\frac {1}{2}}(q_{A}+q_{B}+\beta _{AB}+\beta _{BA})=q+\beta .\end{aligned}}$

Since A and B are identical atoms equipped with identical AOs, we were allowed to use

$\langle 1s_{A}|h|1s_{A}\rangle =q_{A}=q_{B}=q=E_{1s}\quad {\hbox{and}}\quad \langle 1s_{A}|h|1s_{B}\rangle =\beta _{AB}=\beta _{BA}=\beta .$

Likewise

$E_{\sigma _{u}}=\langle \sigma _{u}|h|\sigma _{u}\rangle =q-\beta .$

The energy term β is negative (causes the attraction between the atoms). One may tempted to assume that q = −½ hartree (the energy of the 1s orbital in the free atom). This is not the case, however, because h contains the attraction with both nuclei, so that q is distance dependent.

If we now look at the figure in which energies are increasing in vertical direction, we see that the two AOs are at the same energy level q, and that the energy of σ_g is a distance |β| below this level, while the energy of σ_u is a distance |β| above this level. In the present simple-minded effective-one-electron model we can simply add the orbital energies and find that the bonding energy in H₂ is 2β (two electrons in the bonding MO σ_g, ignoring the distance dependence of q). This model predicts that the bonding energy in the one-electron ion H₂⁺ is half that of H₂, which is correct within a 20% margin.

If we apply the model to He₂, which has four electrons, we find that we must place two electrons in the bonding orbital and two electrons in the antibonding MO σ_u, with the total energy being 2β − 2β = 0. So, this simple application of molecular orbital theory predicts that H₂ is bound and that He₂ is not, which is in agreement with the observed facts.

Atomic orbital basis sets

As stated above, in computational quantum chemistry atomic orbitals are used as a mathematical device to obtain good approximations of N-electron molecular wave functions—solutions of the time-independent electronic Schrödinger equation.

A computation of a molecular wave function usually goes through the following steps:

1. A geometry of the molecule is chosen (in accordance with the Born-Oppenheimer approximation the nuclei are clamped in space).
2. A set of AOs is chosen which are centered on the nuclei. Sometimes the AO set is augmented with orbitals in the middle of bonds, where there are no nuclei. Preferably the AO basis set is as close as possible to a complete basis of one-electron Hilbert space, ${\scriptstyle L^{2}[\mathbb {R} ^{3}]}$, but computer time is a practical limit. (Many methods require computer times proportional to n⁶ or n⁷, where n is the number of AOs.)
3. An LCAO Hartree-Fock calculation yields the MO coefficients c_{A i} and the same number of MOs as AOs (namely n).
4. The MOs are used in a post-Hartree-Fock calculation (configuration interaction, Møller-Plesset perturbation theory, coupled cluster theory, etc.).

The AOs and MOs spanning the very same orbital subspace of one-electron Hilbert space, it would be conceivable to skip the Hartree-Fock calculation. However, it turns out that the post-Hartree-Fock methods converge much better when they are based on MOs instead of on (orthogonalized) AOs.

The size of an AO basis is of crucial importance. The qualitative, pre-computer, MO-theoretical studies were invariably based on minimum basis sets. That is, only orbitals occupied in the free atoms were included in the basis. (But note that, for instance for the ground state boron atom with its electron configuration 1s²2s²2p, it cannot be said whether 2p_x, 2p_y, or 2p_z is occupied. In such a case all three degenerate p orbitals are included in the minimum basis set). It was natural that the first computer calculations followed this pattern and applied minimum basis sets. However, it soon was found that such basis sets give very disappointing results. After this became clear in the late 1960s and early 1970s, search for good AO basis became an important subject of research.

For the mathematical definition of basis sets, we refer to the article Gauss type orbitals (GTOs), because the majority of present-day computer programs handle only GTOs. In the GTO article the concepts of primitive orbital and contracted set are introduced. In a minimum GTO basis set (also known as a single-zeta basis set) every atomic orbital occupied in the free atom is represented by a single contracted set. The term "single-zeta" is historic and refers back to the days that Slater type orbitals were universally used and to the fact that the screening constant in an STO is conventionally indicated by the Greek letter zeta (ζ). Single-zeta (SZ) basis sets giving poor quantitative results, the next step is the use of double-zeta (DZ) basis set, which involves a doubling of the SZ basis. Triple-zeta (TZ) (tripling of the minimum basis), quadruple-zeta (QZ), quintuple-zeta (5Z), sextuple-zeta (6Z) basis sets all have been proposed and have been constructed.

For instance a QZ GTO basis for HCN includes : 4 s-orbitals (s-type contracted sets) on H, 8 s-orbitals on both C and N, 4 p_x-, 4 p_y-, and 4 p_z-orbitals on C and N. In all these cases the construction of the contracted set (AO) involves the determination of the exponents of the primitive Gaussians and the corresponding contraction coefficients.

It is known that an atom polarizes (gets a dipole moment) under influence of an external electric field. It is also known that, in the presence of such a field, AOs of higher l quantum numbers must be included in the basis in order to obtain reliable results. When, for instance, the ground state boron atom (1s²2s²2p) is polarized, there will be a mixing, linear in the strength of the external field, between 2p and 3d. That is, to describe the polarization of the boron atom correctly, one or more 3d sets (sets of five degenerate AOs) must be added to the basis of boron. Since in molecules strong electric fields, due to the nuclei, are present, it stands to reason that polarization functions improve the computational results. For an atom that only has occupied s orbitals, like hydrogen and helium, polarization functions start at l = 1. For atoms such as boron with occupied p-orbitals, the polarization functions are by definition d, f, g, etc. orbitals.

As a final conclusion it must be pointed out that the present-day elaborate AO bases do not have the physical meaning that was attached to AOs in precomputer times. The AOs are now looked upon as building bricks in a numerical approximation, no chemical of physical conclusions are to be drawn from the AOs themselves. The relevant conclusions about nature emerge from the final computational results. Especially in the post Hartree-Fock methods, the contribution of the AOs to the conclusions is deeply hidden in the output and not at all transparent.