Gamma function

The gamma function is a mathematical function that extends the domain of factorials to non-integers. The factorial of a positive integer n, written n!, is the product 1·2·3···n. The gamma function, denoted by $\Gamma$, is defined to satisfy $\Gamma (n)=(n-1)!$ for all positive integers n and to smoothly interpolate the factorial between the integers. The gamma function is one of the most commonly occurring examples of a nonelementary function; that is, a function that cannot be expressed in finite terms using algebraic operations, exponentials, and logarithms. Its study dates back to Leonhard Euler, who gave a formula for its calculation in 1729.

Definition and basic properties

The product $1\cdot 2\cdot ...\cdot n$ cannot be expressed in closed form using only regular arithmetic operations and elementary functions. This is perhaps surprising, since the analogous sum $1+2+...+n$ is simply $n(n+1)/2$, a triangular number. To find a closed-form expression for factorials, it is necessary to deploy tools from calculus. In modern treatments, the gamma function is usually defined using Euler's integral,

$\Gamma (z)=\int _{0}^{\infty }e^{-t}t^{z-1}dt.$

It is a slight technicality to prove that this integral defines a well-behaved function and to determine its domain. It is easy to see that the integral converges if z is a positive real number or a complex number with positive real part. In fact, the integral defines an analytic function in the positive complex half-plane. Then, the definition of the function can be extended to the rest of the plane as well using the analytic continuation. We will give the continuation explicitly in a moment.

To see why we are justified in calling the gamma function as defined above an extension of the factorial, we insert z+1 instead of z and perform an integration by parts to obtain

$\Gamma (z+1)=\left[-e^{-t}t^{z}\right]_{0}^{\infty }+z\int _{0}^{\infty }e^{-t}t^{z-1}dt=z\Gamma (z).$

This relation is called the functional equation of the gamma function. It is analogous to the recurrence formula for the factorial, $n!=n(n-1)!$, the only difference being that the function argument has been shifted by 1. More generally, a repeated application of the functional equation gives

$\Gamma (z+n)=z(z+1)(z+2)\cdots (z+n-1)\Gamma (z).$

With the initial value $\textstyle \Gamma (1)=\int _{0}^{\infty }e^{-t}dt=1=0!$, this establishes that

$\Gamma (n)=1\cdot 2\cdot 3\ldots (n-1)=(n-1)!$

for positive natural numbers n, or equivalently, that $\Gamma (n+1)=n!$. We may use these formulas to explicitly calculate $\Gamma (n)$ or, conversely, to define z! for non-integers in terms of the gamma function.

The above functional equation allows us to extend our definition to the entire complex plane, including negative real numbers for which, formally, the Euler's integral does not converge. Indeed, by rewriting the equation as

$\Gamma (z)={\frac {\Gamma (z+n)}{z(z+1)\cdots (z+n-1)}},$

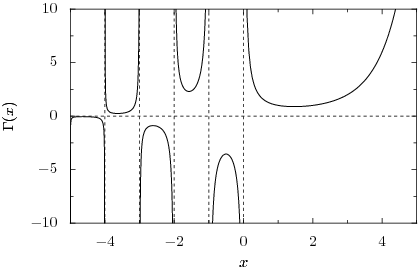
which we might call the forward recurrence relation, and choosing n such that z+n lies in the positive half-plane, we can formally compute $\Gamma (z)$ for z different from $0,-1,-2,\ldots$ (the right-hand side blows up, so the gamma function must be undefined at these points). Clearly, our extension defines an analytic function everywhere else. Therefore, by uniqueness, it is the above mentioned analytic continuation of the Euler integral. It follows that the gamma function is a meromorphic function with poles at the nonpositive integers. The following image shows the graph of the gamma function along the real line:

The gamma function is nonzero everywhere along the real line, although it comes arbitrarily close as $z\to -\infty$. There is in fact no complex number z for which $\Gamma (z)=0$, and hence the reciprocal gamma function $1/\Gamma$ is an entire function, with zeros at $z=0,-1,-2,\ldots$. We see that the gamma function has a local minimum at $x_{\mathrm {min} }\approx 1.46163$ where it attains the value $\Gamma (x_{\mathrm {min} })\approx 0.885603$. The gamma function must alternate sign between the poles because the product in the forward recurrence contains an odd number of negative factors if the number of poles between z and z+n is odd, and an even number if the number of poles is even.

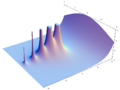
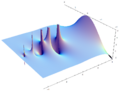
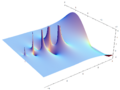
Plotting the gamma function in the complex plane yields beautiful graphs:

• 

  Absolute value

• 

  Real part

• 

  Imaginary part

A final basic but important property of the gamma function is the reflection formula

$\Gamma (z)\Gamma (1-z)={\frac {\pi }{\sin \pi z}}$

which gives a concise relation between the gamma function of positive and negative numbers. The division by a sine, which is periodically zero, again indicates the existence of the gamma function's periodically occurring poles. Further, inserting z = 1/2 reveals the surprising fact that

$\Gamma (1/2)={\sqrt {\pi }}.$

Hence, by the recurrence formula, the gamma function or factorial of any half-integer is a rational multiple of ${\sqrt {\pi }}$.

History, notation, and alternative definitions

The problem of extending the factorial to non-integer arguments was apparently first proposed by Daniel Bernoulli and Christian Goldbach in the 1720s. Leonhard Euler wrote to Goldbach on October 13, 1729 to announce that he had found a solution,

$n!=\lim _{m\to \infty }{\frac {m^{n}m!}{(n+1)(n+2)\cdots (n+m)}}.$

The following year, on January 8, 1730, he again wrote to Goldbach to reveal that, for n > 0, the formula

$n!=\int _{0}^{1}(-\log t)^{n}\,dt$

is a solution. This is in fact simply Euler's integral with a change of variables.

The problem of finding a continuous expression for the factorial was also considered by James Stirling, who in Methodus Differentialis (1730) published the famous Stirling's formula

$n!\approx {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}$

Although Stirling's formula gives a good estimate of n!, also for non-integers, it does not provide the exact value. Stirling made several attempts to refine his approximation, and eventually found a solution, although he never managed to prove that the extended version of his formula indeed corresponds exactly to the factorial. A proof was first given by Charles Hermite in 1900.

In conclusion, there have been several independent attempts to characterize the gamma function. We used Euler's integral as a starting point in this article, but it is not entirely uncommon for authors to start with Euler's original (1729) representation. Are these approaches compatible? Euler himself does not appear to have proved that he had found a unique solution.

There are in fact infinitely many ways to extend the factorial, but the gamma function is the unique analytic solution, subject to the additional condition of being logarithmically convex for positive arguments. This fact was first proved by Harald Bohr and Johannes Mollerup in 1922 and is now known as the Bohr-Mollerup theorem.

The name gamma function and the symbol $\Gamma$ were introduced by Adrien-Marie Legendre around 1811. Although the symbol is an upper-case Greek Gamma, there is no accepted standard for whether the function name should be written "Gamma function" or "gamma function" (some authors simply write "$\Gamma$-function"). The alternative "Pi function" notation $\Pi (z)=z!$ due to Carl Friedrich Gauss is sometimes encountered in older literature, but Legendre's notation is dominant in modern works.

It is justified to ask why we distinguish between the "ordinary factorial" and the gamma function by using distinct symbols, and particularly why the gamma function should be normalized to $\Gamma (n+1)=n!$ instead of simply using "$\Gamma (n)=n!$". Legendre's motivation for the normalization does not appear to be known, and has been criticized as cumbersome by some mathematicians (Cornelius Lanczos, for example, called it "void of any rationality" and used $z!$ instead). The normalization does simplify some formulas, but complicates others.

Derivatives, products, and connection to Euler's constant

Many of the important special functions in mathematics, such as Bessel functions and orthogonal polynomials, are defined in terms of differential equations. The gamma function is characterized by functional equations such as the recurrence formula, but it is unusual among the classical special functions in that it does not appear to satisfy any simple differential equation. The term "simple" can be qualified: Otto Hölder proved in 1887 that the gamma function does not satisfy any algebraic differential equation whose coefficients are rational functions. This theorem, known as Hölder's theorem, has later been given alternative proofs and generalized by several other mathematicians.

Nonetheless, the derivatives of the gamma function are important special functions in their own right. The logarithmic derivatives of the gamma function are called polygamma functions (of order m), denoted by $\psi ^{m}$. They are given by

${\frac {d^{m}}{dz^{m}}}\log \Gamma (z)=\psi ^{(m-1)}(z).$

In particular, the first derivative of the gamma function is given in terms of the zeroth-order polygamma function (also called the digamma function) by

$\Gamma '(z)=\Gamma (z)\,\psi ^{(0)}(z)$

and the derivative at an integer is

$\Gamma '(n+1)=n!\,\left(1+{\frac {1}{2}}+{\frac {1}{3}}+\ldots +{\frac {1}{n}}-\gamma \right)$

where $\gamma \approx 0.577216$ is Euler's constant. As a special case, we have $\Gamma '(1)=-\gamma$, which provides a geometric interpretation of Euler's constant as the slope of the gamma function's graph at 1.

Relation to the Riemann zeta function

An important property of the Riemann zeta function is its functional equation:

$\Gamma ({\frac {s}{2}})\pi ^{-{\frac {s}{2}}}\zeta (s)=\Gamma ({\frac {1-s}{2}})\pi ^{-{\frac {1-s}{2}}}\zeta (1-s)$

Among other things, this provides an explicit form for the analytic continuation of the zeta function to a meromorphic function in the complex plane.

Use in integration

Frequently encountered generalizations of the gamma function include the incomplete gamma functions

$\Gamma (a,x)=\int _{x}^{\infty }t^{a-1}\,e^{-t}\,dt\,\!$

$\gamma (a,x)=\int _{0}^{x}t^{a-1}\,e^{-t}\,dt.\,\!$

and the beta function

$\mathrm {\mathrm {B} } (x,y)={\frac {\Gamma (x)\,\Gamma (y)}{\Gamma (x+y)}}.$

A variety of definite and indefinite integrals whose solutions are nonelementary can be expressed in terms of some combination of gamma functions and incomplete gamma functions. An example is that the Laplace transform of the power function x^c reduces to the Euler integral and hence the gamma function. Watson's triple integrals provide a more complicated example.

Integrands involving powers are particularly often susceptible to evaluation in terms of gamma functions, as it may be possible to consider the exponent an integer, eliminate it by repeated integration by parts to obtain a factorial times a solvable integral, and generalizing the result to arbitrary complex exponents by replacing the factorial with a gamma function. At other times, it is possible to directly transform an integral into an Euler integral by an appropriate change of variables.

Viewed as a non-elementary integral of an elementary function, the gamma function belongs to the same category of special functions as the error function, the exponential integral, the logarithmic integral, and the sine integral. There are many known interrelations between these functions and the gamma function.

The gamma function is also important in the theory of hypergeometric functions, the Meijer G-function and the Fox H-function. The G and H-functions are defined in terms of Mellin-Barnes integrals which are certain complex contour integrals of products of gamma functions.

Miscellaneous applications

An illustrative example of the consequences of being able to extend the factorial to non-integers is that of the fractional derivative. According to Cauchy's integral formula, the ordinary nth derivative of a function f is given by

$f^{(n)}(a)={n! \over 2\pi i}\oint _{C}{f(z) \over (z-a)^{n+1}}\,dz.$

Replacing n! with Γ(n+1), it becomes possible to calculate "derivatives" of fractional order. The gamma function is also used to express Bessel functions of fractional order and gives a general formula for area and volume of an n-dimensional hypersphere.

The gamma function can be used to express many types of products besides the ordinary factorial, such as multiple factorials, Pochhammer symbols and binomial coefficients. For a monic polynomial P with roots p₁...p_n, one has the general formula

$\prod _{j=a}^{b}P(j)=\prod _{k=1}^{n}{\frac {\Gamma (b-p_{k}+1)}{\Gamma (a-p_{k})}},$

which in turn can be generalized to a formula for quotients of polynomials. Summation of series where each term is a rational function of the running index can be performed in an analogous manner using polygamma functions.

The gamma function is also used in statistics to define the gamma distribution, the inverse-gamma distribution, and the beta distribution.

Calculation

Although the gamma function cannot be expressed exactly in terms of elementary functions, the graphs and numerical values given in this article imply the existence of methods for its numerical calculation. One straightforward approach would be to perform numerical integration of Euler's integral, but there are more efficient methods. The most popular is an extended version of Stirling's formula known as Stirling's series

$\Gamma (z+1)\sim {\sqrt {2\pi z}}\left({\frac {z}{e}}\right)^{z}\left(1+{\frac {1}{12z}}+{\frac {1}{288z^{2}}}-\cdots \right)$

where the coefficients in the series can be calculated analytically in terms of Bernoulli numbers. The "$\sim$" sign in this formula denotes an asymptotic equality: the series diverges for every z, but yields arbitrarily accurate approximations of the gamma function as $z\to \infty$ if truncated appropriately. A practical way to calculate the gamma function is to calculate $\Gamma (z+n)$ for some large integer n using Stirling's series and then repeatedly apply the recurrence formula to obtain $\Gamma (z)$. Taking $n=10$ and including the three first terms in Stirling's series, we obtain

$\Gamma (1)\approx 1.00000267$

$\Gamma (2)\approx 1.00000201$

This particular approximation is good to five decimal places on the interval [1, 2]. With larger n and more terms, Stirling's formula can be used to calculate the gamma function with arbitrary precision. Other practical methods include the Lanczos approximation and Spouge's approximation.

In general, the following properties of the gamma function are useful to have in mind for numerical calculations:

• Due to the recurrence formula, the gamma function can be calculated anywhere in the complex plane if it can be calculated in some region with real part in $[x,x+1]$.
• If the gamma function can be calculated in the positive half-plane, the reflection formula permits its computation in the negative half-plane as well.
• It may be convenient to work with the logarithm of the gamma function to avoid overflow for large arguments. It is common to encounter a quotient of two gamma functions, which are best computed by subtracting logarithms.

Double-precision (16-digit) floating-point implementations of the gamma function are available in most scientific computing software and special functions libraries, for example Matlab, GNU Octave, and the GNU Scientific Library. The gamma function was also added to the C mathematics library (math.h) as part of the C99 standard, but is not implemented by all C compilers. Arbitrary-precision implementations are available in most computer algebra systems, such as Mathematica and Maple. Pari/GP and MPFR provide free arbitrary-precision implementations.