Euler angles

From Citizendium
Revision as of 04:01, 12 July 2009 by imported>Paul Wormer
Jump to navigation Jump to search

(Under construction, please leave alone)

PD Image
Figure 1. Euler angles. From left to right: initial configuration, after rotation over angle α, after rotation over angle β, and after rotation over angle γ.

In physics, mathematics, and engineering, Euler angles are three rotation angles, commonly denoted by 0 ≤ α ≤ 2π, 0 ≤ β ≤ π, and 0 ≤ γ ≤ 2π. Any rotation of a 3-dimensional object can be performed by three consecutive rotations over the three Euler angles.

Different conventions are in use: a rotation can be active (the object is rotated, the system of axes is fixed in space), or passive (the object is fixed in space, the axes are rotated).

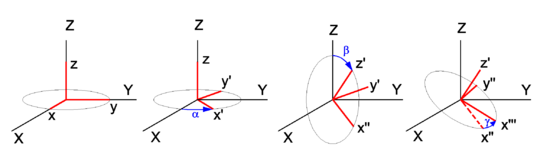
The choice of rotation axes may vary; a very common active convention is the z-y′-z′ convention. Attach a system of Cartesian coordinate axes to the body that is to be rotated (the coordinate frame is fixed to the body and is rotated simultaneously with it); in the figure the body-fixed frame is shown in red and labeled by lowercase letters. First rotate around z, then around the new body-fixed y-axis, y′, and finally around z′. Another convention often used is the z-x′-z′ convention, where instead of over the new y-axis the second rotation is over the new x-axis. Also the x-y′-z′′ convention is used.

The right-hand screw rule is practically always followed: the rotation axis is a directed line and a positive rotation is as a cork screw driven into the positive direction of the axis.

Euler angles are used in many different branches of physics and engineering. The present article is written from the point of view of molecular physics, where the objects to be rotated are molecules.

Geometric discussion

In Figure 1 the space-fixed (laboratory) axes are labeled by capital X, Y, and Z and are shown in black. The body to be rotated is not shown, but a system of axes fixed to it is shown in red. One may use any convenient orthonormal frame as a body-fixed frame. Often the body-fixed axes are principal axes, that means that they are eigenvectors of the inertia tensor of the body. Also symmetry axes, when present, may be used. When the body has symmetry axes, the principal axes often coincide with these.

PD Image
Figure 2. Rotation of r to r′. On the left around z-axis over α (φ increases), on the right around y-axis over β (φ decreases). Both rotation axes point toward the reader.

The z-y′-z′ convention will be followed. Initially, the two frames coincide, and the path to a final arbitrary orientation of the body—and its frame—is depicted on Figure 1. The first rotation is around the z-axis, which coincides with the Z-axis. The x- and y-axis move in a plane perpendicular to the z-axis over an angle α. The second rotation is in a plane through the origin perpendicular to the y′-axis. The angle is β. The present convention has the great practical advantage that the z′-axis has the usual spherical polar coordinates α ≡ φ (longitude angle) and β ≡ θ (colatitude angle) with respect to the space-fixed frame. (For instance, due to this fact the complex conjugate of the m = 0 column of the Wigner D-matrix consists of spherical harmonics). The final rotation is in a plane perpendicular to the z′-axis over an angle γ. From geometric considerations follows that any orientation of the body-fixed frame in space may be obtained.

Write Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{R}(\varphi, \hat{n})} for the rotation matrix that describes a rotation around the unit vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{n}} over an angle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varphi} . Clearly the three consecutive Euler rotations correspond to rotations around the unit vectors along the body-fixed axes z, y′, and z′ over angles α β, and γ, respectively. Because a matrix acts on a column vector to its right, the order in the matrix product is as in the leftmost term in the following equation. It will be shown that the corresponding matrix product can be written in reverse order (but around fixed, unprimed, axes z, y, z), that is,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \mathbf{R}(\gamma, \hat{e}_{z'}) \mathbf{R}(\beta, \hat{e}_{y'}) \mathbf{R}(\alpha, \hat{e}_{z})&= \mathbf{R}(\alpha, \hat{e}_{z }) \mathbf{R}(\beta, \hat{e}_{y }) \mathbf{R}(\gamma, \hat{e}_{z}) \\ &= \begin{pmatrix} \cos\alpha & -\sin \alpha & 0 \\ \sin\alpha & \cos \alpha & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} \begin{pmatrix} \cos\beta & 0 & \sin\beta \\ 0 & 1 & 0 \\ -\sin\beta & 0 & \cos\beta \\ \end{pmatrix} \begin{pmatrix} \cos\gamma & -\sin\gamma & 0 \\ \sin\gamma & \cos\gamma & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} \\ &= \begin{pmatrix} \cos\alpha\cos\beta\cos\gamma-\sin\alpha\cos\gamma \;&\; -\cos\alpha\cos\beta\sin\gamma-\sin\alpha\cos\gamma \;&\;\cos\alpha\sin\beta \\ \sin\alpha\cos\beta\cos\gamma+\cos\alpha\sin\gamma \;&\; -\sin\alpha\cos\beta\sin\gamma+\cos\alpha\cos\gamma \;&\; \sin\alpha\sin\beta \\ -\sin\beta\cos\gamma \;&\; \sin\beta\sin\gamma \;&\; \cos\beta \end{pmatrix} \end{align} }

Before proving the first equality in the above equation (reversal of order), we derive the matrix for a rotation around the z-axis, see the left drawing in Figure 2. The rotated vector has components

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{pmatrix} \cos(\alpha + \phi) \\ \sin(\alpha + \phi) \\ 0 \end{pmatrix} = \begin{pmatrix} \cos\alpha\cos\phi -\sin\alpha\sin\phi \\ \sin\alpha\cos\phi + \cos\alpha\sin\phi \\ 0 \end{pmatrix} = \begin{pmatrix} \cos\alpha & -\sin\alpha & 0 \\ \sin\alpha & \cos\alpha & 0\\ 0 & 0 & 1 \\ \end{pmatrix} \begin{pmatrix} \cos\phi \\ \sin\phi \\ 0 \\ \end{pmatrix} \equiv \mathbf{R}(\alpha, \hat{e}_z) \begin{pmatrix} \cos\phi \\ \sin\phi \\ 0 \end{pmatrix} . }

We used here the relations well-known from trigonometry for the sine and cosine of a sum angle. The derivation of the matrix for a rotation around the y-axis proceeds along the same lines. Note, however, that the angle of a vector with the x-axis decreases by a rotation around the positive y-axis (see right-hand drawing in Figure 2).

To prove the first equality (reversal of the order in the angles), a property of rotation matrices is used. A rotation (orthogonal 3×3) matrix A, transforming a rotation axis, gives rise to the following similarity equation,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{R}(\varphi, \mathbf{A}\hat{n}) = \mathbf{A}\mathbf{R}(\varphi, \hat{n})\mathbf{A}^{\mathrm{T}}, }

where the superscript T indicates the transpose of the matrix. For rotation matrices the transposed matrix is equal to the inverse of the matrix. From this similarity relation follows that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{R}(\gamma, \hat{e}_{z'}) = \mathbf{R}(\beta, \hat{e}_{y'}) \mathbf{R}(\gamma, \hat{e}_{z}) \mathbf{R}(\beta, \hat{e}_{y'})^{\mathrm{T}}, }

so that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{R}(\gamma, \hat{e}_{z'}) \mathbf{R}(\beta, \hat{e}_{y'}) \mathbf{R}(\alpha, \hat{e}_{z})= \mathbf{R}(\beta, \hat{e}_{y'}) \mathbf{R}(\gamma, \hat{e}_{z}) \mathbf{R}(\beta, \hat{e}_{y'})^{\mathrm{T}} \; \mathbf{R}(\beta, \hat{e}_{y'}) \mathbf{R}(\alpha, \hat{e}_{z}) = \mathbf{R}(\beta, \hat{e}_{y'}) \mathbf{R}(\gamma, \hat{e}_{z}) \mathbf{R}(\alpha, \hat{e}_{z}). }

Also

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{R}(\beta, \hat{e}_{y'}) = \mathbf{R}(\alpha, \hat{e}_{z})\mathbf{R}(\beta, \hat{e}_{y})\mathbf{R}(\alpha, \hat{e}_{z})^{\mathrm{T}}, }

so that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{R}(\beta, \hat{e}_{y'}) \mathbf{R}(\gamma, \hat{e}_{z}) \mathbf{R}(\alpha, \hat{e}_{z}) = \mathbf{R}(\alpha, \hat{e}_{z})\mathbf{R}(\beta, \hat{e}_{y}) \mathbf{R}(\alpha, \hat{e}_{z})^{\mathrm{T}} \; \mathbf{R}(\gamma, \hat{e}_{z}) \mathbf{R}(\alpha, \hat{e}_{z}) = \mathbf{R}(\alpha, \hat{e}_{z})\mathbf{R}(\beta, \hat{e}_{y}) \mathbf{R}(\gamma, \hat{e}_{z}), }

where it is used that rotations around the same axis commute, that is,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{R}(\alpha, \hat{e}_{z})^{\mathrm{T}} \mathbf{R}(\gamma, \hat{e}_{z}) \mathbf{R}(\alpha, \hat{e}_{z}) = \mathbf{R}(\gamma, \hat{e}_{z}) \mathbf{R}(\alpha, \hat{e}_{z})^{\mathrm{T}} \mathbf{R}(\alpha, \hat{e}_{z}) = \mathbf{R}(\gamma, \hat{e}_{z}) }

and the required result is proved.

Algebraic treatment

In the proof that any rotation can be written as three consecutive rotations an appeal was made to the geometric insight of the reader. This result can be proved more rigorously by algebraic means. The notation is somewhat shortened:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{R}(\omega, \hat{e}_{z}) \equiv \mathbf{R}_z (\omega) \quad\hbox{and}\quad \mathbf{R}(\omega, \hat{e}_{y}) \equiv \mathbf{R}_y (\omega ). }

Theorem

A proper rotation matrix R can be factorized thus

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{R} = \mathbf{R}_z (\omega_3 ) \; \mathbf{R}_y (\omega_2 ) \; \mathbf{R}_x (\omega_1 ) }

which is referred to as the Euler z-y-x parametrization, or also as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{R} = \mathbf{R}_z (\alpha) \; \mathbf{R}_y (\beta ) \; \mathbf{R}_z (\gamma ) \quad }

the Euler z-y-z parametrization.

Proof

First the Euler z-y-x-parametrization will be proved by an algorithm for the factorization of a given matrix R. Consider the matrix product

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{R}_z (\omega_3 ) \, \mathbf{R}_y (\omega_2 ) = \begin{pmatrix} \cos \omega_3 \cos \omega_2 & -\sin \omega_3 & \cos \omega_3 \sin \omega_2 \\ \sin \omega_3 \cos \omega_2 & \cos \omega_3 & \sin \omega_3 \sin \omega_2 \\ -\sin \omega_2 & 0 & \cos \omega_2 \\ \end{pmatrix} \equiv (\mathbf{a}_1 , \mathbf{a}_2 , \mathbf{a}_3 ) . }

The columns of the matrix product are for ease of reference designated by a1, a2, and a3. Note that the multiplication by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{R}_x(\omega_1) \equiv \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos\omega_1 & -\sin\omega_1 \\ 0 & \sin\omega_1 & \cos\omega_1 \end{pmatrix} }

on the right does not affect the first column, so that a1 = r1 (the first column of R). Solve Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_2\;} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_3\;} from the first column of R,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{a}_1 = \begin{pmatrix} \cos \omega_3 \; \cos \omega_2 \\ \sin \omega_3 \; \cos \omega_2 \\ -\sin \omega_2 \\ \end{pmatrix} = \begin{pmatrix} R_{11} \\ R_{21} \\ R_{31} \\ \end{pmatrix} \equiv \mathbf{r}_1 . }

This is possible. First solve Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_2\;} for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\pi/2 \leq \omega_2 \leq \pi/2} from

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sin \omega_2 = - R_{31}. \, }

Then solve Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_3\;} for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 \leq \omega_3 \leq 2 \pi} from the two equations:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \cos \omega_3 =& {R_{11} \over \cos \omega_2} \\ \sin \omega_3 =& {R_{21} \over \cos \omega_2} . \end{align} }

Knowledge of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_2\;} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_3\;} determines the vectors a2 and a3.

Since a1, a2 and a3 are the columns of a proper rotation matrix they form an orthonormal right-handed system. The plane spanned by a2 and a3 is orthogonal to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{a}_1 \equiv \mathbf{r}_1} and hence the plane contains Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}_2} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}_3} . Thus the latter two vectors are a linear combination of the first two,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ( \mathbf{r}_2 , \mathbf{r}_3 ) = (\mathbf{a}_2 , \mathbf{a}_3 ) \begin{pmatrix} \cos \omega_1 & -\sin \omega_1 \\ \sin \omega_1 & \cos \omega_1 \\ \end{pmatrix} . }

Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}_2,\; \mathbf{a}_2,\; \mathbf{a}_3} are known unit vectors we can compute

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \mathbf{a}_2 \cdot \mathbf{r}_2 =& \cos \omega_1 \\ \mathbf{a}_3 \cdot \mathbf{r}_2 =& \sin \omega_1. \end{align} }

These equations give Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_1\;} with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 \leq \omega_1 \leq 2 \pi} .

Augment the 2×2 matrix to the 3×3 matrix Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{R}_x(\omega_1)} , then

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \mathbf{R} \equiv ( \mathbf{r}_1 , \mathbf{r}_2 , \mathbf{r}_3 ) = ( \mathbf{r}_1 , \mathbf{a}_2 , \mathbf{a}_3 ) \mathbf{R}_x (\omega_1 ) = (\mathbf{a}_1, \mathbf{a}_2, \mathbf{a}_3)\mathbf{R}_x (\omega_1 ) = \mathbf{R}_z (\omega_3 ) \, \mathbf{R}_y (\omega_2 ) \, \mathbf{R}_x (\omega_1 ) . \end{align} }

This concludes the proof of the Euler z-y-x parametrization.

The Euler z-y-z parametrization is obtained by a small modification of the previous proof. Solve Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_2\;} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_3\;} from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}_3 = \mathbf{a}_3 } (the rightmost multiplication by Rz(ω1) does not affect r3) and then consider

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ( \mathbf{r}_1, \; \mathbf{r}_2 ) = (\mathbf{a}_1, \; \mathbf{a}_2 ) \begin{pmatrix} \cos \omega_1 & -\sin \omega_1 \\ \sin \omega_1 & \cos \omega_1 \\ \end{pmatrix} }

or, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{a}_1 \cdot \mathbf{r}_1 = \cos \omega_1 \; , \quad \mathbf{a}_2 \cdot \mathbf{r}_1 = \sin \omega_1 . } The equation for R can be written as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ( \mathbf{r}_1 , \mathbf{r}_2 , \mathbf{r}_3 ) = ( \mathbf{a}_1 , \mathbf{a}_2 , \mathbf{r}_3 ) \, \mathbf{R}_z (\omega_1 ) = \mathbf{R}_z (\omega_3 ) \, \mathbf{R}_y (\omega_2 ) \, \mathbf{R}_z (\omega_1 ) \; , }

which proves the Euler z-y-z parametrization. Clearly, this factorization is equal to the one given earlier, where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_3 = \alpha,\quad \omega_2 = \beta, \quad \omega_1 = \gamma. }


(To be continued)

Retrieved from "https://citizendium.org/wiki/index.php?title=Euler_angles&oldid=636443"