User:David MacQuigg/Sandbox/Shortest path routing
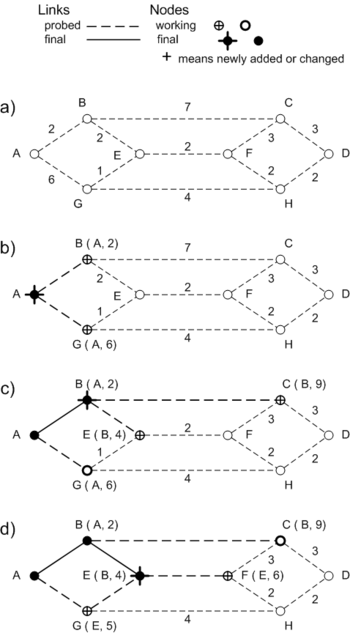
<pre> # dijkstra59v03.py Shortest Path Routing DMQ 12/15/09 ''' Use Dijkstra's algorithm to compute the shortest paths from a given source node to all other nodes in a network. Links are bi-directional, with the same distance in either direction. ''' # Example from Figure 1 (8 nodes, 11 links) nodeset = {'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H'} linklist = [('A', 'B', 2), ('B', 'C', 7), ('C', 'D', 3), # (node,node,distance) ('B', 'E', 2), ('E', 'F', 2), ('F', 'C', 3), ('A', 'G', 6), ('G', 'E', 1), ('G', 'H', 4), ('F', 'H', 2), ('H', 'D', 2), ] INF = int(1e9) # larger than any possible path def get_anodes(nodeset, linklist): '''Create a dictionary to quickly look up the adjacent nodes for any given node. >>> get_anodes(nodeset, linklist) {'A': {('B', 2), ('G', 6)}, 'C': {('B', 7), ('F', 3), ('D', 3)}, \ 'B': {('C', 7), ('E', 2), ('A', 2)}, 'E': {('B', 2), ('G', 1), ('F', 2)}, \ 'D': {('H', 2), ('C', 3)}, 'G': {('A', 6), ('E', 1), ('H', 4)}, \ 'F': {('H', 2), ('E', 2), ('C', 3)}, 'H': {('G', 4), ('D', 2), ('F', 2)}} ''' anodes = {} # An empty dictionary to start for n in nodeset: lnks = set() # set of links to each node, initially none for (n1, n2, x) in linklist: # scan for links connected to n if n1 == n: lnks.add((n2, x)) if n2 == n: lnks.add((n1, x)) anodes[n] = lnks # all the links to node n return anodes def build_tree(src, anodes): '''Given a source node and a table of adjacent nodes for every node in a network, return a table with two values for each node - the distance on the shortest path from the source to that node, and the name of the next-to-last node on that path. >>> build_tree('A', anodes) {'A': ('A', 0), 'C': ('B', 9), 'B': ('A', 2), 'E': ('B', 4), \ 'D': ('H', 10), 'G': ('E', 5), 'F': ('E', 6), 'H': ('F', 8)} ''' # Current working node, and its distance from src wrk = src; dist = 0 # Nodes in the working set and final set, saved as dictionaries. # {key: value} = {nodename: label} # label = (previous node along path, distance from src) Wset = {}; Fset = {} Fset[wrk] = (wrk, 0) # starting node is always in Fset for (n, d) in anodes[wrk]: label = (wrk, d) Wset[n] = label while Wset: # loop until the working set is empty # Find the shortest distance in the working set, and make that node the # new working node. The distance of that node will never get smaller. dist = INF for node in Wset: d = Wset[node][1] if d < dist: dist = d wrk = node # Move the new working node to the final set. Fset[wrk] = Wset[wrk] del Wset[wrk] # Probe the nodes adjacent to wrk. for (n, d) in anodes[wrk]: new_dist = dist + d if n in Fset: # skip this node, already finalized continue elif (n in Wset) and (new_dist >= Wset[n][1]): continue # skip this probe, too long else: # Add new node to working set, or update existing node. Wset[n] = (wrk, new_dist) return Fset def get_path(src, dest, tree): '''Given source and destination nodes, and the dictionary returned by build_tree(), return the shortest path through the network. >>> get_path('A', 'D', tree) ['A', 'B', 'E', 'F', 'H', 'D'] ''' wrk = dest # Work backward from the destination node. path = [] while wrk != src: path.append(wrk) wrk = tree[wrk][0] # step back to previous node path.append(src) # don't forget to include the source path.reverse() return path </pre>