Lemniscate

PD Image
Blue: lemniscate of Bernoulli (a=1); red: lemniscate of Gerono (a²=2)

.

A lemniscate is a geometric curve in the form of the digit 8, usually drawn such that the digit is lying on its side, as the infinity symbol $\infty$. The name derives from the Greek λημνισκος (lemniskos, woolen band).

Two forms are common.

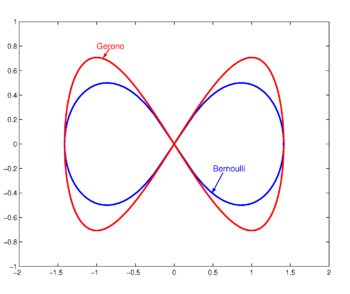
Lemniscate of Gerono

This form is named for the French mathematician Camille Christophe Gerono (1799-1891). Its equation in Cartesian coordinates is

$\ x^{4}=a^{2}(x^{2}-y^{2})$.

The figure shows the case a = √2

Lemniscate of Bernoulli

This form is named for James Bernoulli, who coined the name lemniscata (feminine form of lemniscatus) and published its form in an article in Acta Eruditorum in 1694. Basically, Bernoulli's lemniscate is the locus of points that have a distance r₁ to a focus F₁ and a distance r₂ to a focus F₂, while r₁r₂ is constant. In the figure the foci are on the x-axis at ±1. The product of the distances is constant and equal to half the distance 2a between the foci squared. For foci on the x-axis at ±a the equation is,

$r_{1}\,r_{2}=a^{2}=\left[{\big (}(x-a)^{2}+y^{2}{\big )}{\big (}(x+a)^{2}+y^{2}{\big )}\right]^{\frac {1}{2}}.$

Expanding and simplfying gives

$(x^{2}+y^{2})^{2}=2a^{2}(x^{2}-y^{2}).\;$

The latter equation gives upon substitution of

$x=r\cos \theta ,\quad y=r\sin \theta$

the following polar equation

$r^{4}=2a^{2}r^{2}(\cos ^{2}\theta -\sin ^{2}\theta )\Longrightarrow r^{2}=2a^{2}\cos 2\theta .$