Dirac delta function: Difference between revisions
imported>Paul Wormer |
imported>Paul Wormer No edit summary |
||
| Line 1: | Line 1: | ||
{{subpages}} | {{subpages}} | ||
In [[physics]], the '''Dirac delta function''' is a function introduced by [[Paul Adrien Maurice Dirac|P.A.M. Dirac]] in his seminal 1930 book on quantum mechanics.<ref>P. | In [[physics]], the '''Dirac delta function''' is a function introduced by [[Paul Adrien Maurice Dirac|P. A. M. Dirac]] in his seminal 1930 book on quantum mechanics.<ref>P. A. M. Dirac, ''The Principles of Quantum Mechanics'', Oxford University Press (1930). Fourth edition 1958. Paperback 1981, p. 58</ref> Heuristically, the function can be seen as a generalization of the [[Kronecker delta]] from integral (elements of <font style="vertical-align: 13%"> <math>\mathbb{Z}</math></font>) to real (elements of <font style="vertical-align: 13%"><math>\mathbb{R}</math></font>) indices. | ||
Note that the Kronecker delta acts as a "filter" in a summation: | |||
:<math> | :<math> | ||
\sum_{i= | \sum_{i=m}^n \; f_i\; \delta_{ia} = | ||
\begin{cases} | \begin{cases} | ||
f_a & \quad\hbox{if}\quad a\in[ | f_a & \quad\hbox{if}\quad a\in[m,n] \sub\mathbb{Z} \\ | ||
0 & \quad \hbox{if}\quad a \notin [ | 0 & \quad \hbox{if}\quad a \notin [m,n]. | ||
\end{cases} | \end{cases} | ||
</math> | </math> | ||
In analogy, the Dirac delta function δ(''x''−''a'') is defined by (replace ''i'' by ''x'' and the summation over ''i'' by an integration over ''x''), | |||
:<math> | :<math> | ||
\int_{a_0}^{a_1} f(x) \delta(x-a) \mathrm{d}x = | \int_{a_0}^{a_1} f(x) \delta(x-a) \mathrm{d}x = | ||
\begin{cases} | \begin{cases} | ||
f(a) & \quad\hbox{if}\quad a\in[a_0, | f(a) & \quad\hbox{if}\quad a\in[a_0,a_1] \sub\mathbb{R}, \\ | ||
0 & \quad \hbox{if}\quad a \notin [a_0, | 0 & \quad \hbox{if}\quad a \notin [a_0,a_1]. | ||
\end{cases} | \end{cases} | ||
</math> | </math> | ||
The Dirac delta function is not an ordinary well-behaved map <font style="vertical-align: 12%"><math>\mathbb{R} \rightarrow \mathbb{R}</math></font>, but a [[distribution (mathematics)|distribution]], also known as an ''improper'' or ''generalized function''. Physicists express its special character by stating that the Dirac delta function makes only sense as a factor in an integrand. Mathematicians say that the delta function is a linear functional on a space of test functions. | |||
The Dirac delta function is ''not'' an ordinary well-behaved map <font style="vertical-align: 12%"><math>\mathbb{R} \rightarrow \mathbb{R}</math></font>, but a [[distribution (mathematics)|distribution]], also known as an ''improper'' or ''generalized function''. Physicists express its special character by stating that the Dirac delta function makes only sense as a factor in an integrand ("under the integral"). Mathematicians say that the delta function is a linear functional on a space of test functions. | |||
==Properties== | ==Properties== | ||
| Line 30: | Line 34: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
The physicist's proof of these properties proceeds by making proper substitutions into the integral and using the ordinary rules of integral calculus. | The physicist's proof of these properties proceeds by making proper substitutions into the integral and using the ordinary rules of integral calculus. | ||
The last property is the analogy of the multiplication of two [[identity matrix|identity matrices]], | |||
:<math> | |||
\sum_{j=1}^n \;\delta_{ij}\;\delta_{jk} = \delta_{ik}, \quad i,k=1,\ldots, n. | |||
</math> | |||
==Delta-convergent sequences== | ==Delta-convergent sequences== | ||
There exist families of regular functions of which the family members differ by the value of a single parameter α. An example is the family of | There exist families of regular functions of which the family members differ by the value of a single parameter α. An example of such a family is formed by the family of [[Gaussian function]]s ''F''<sub>α</sub>(''x'') = exp(−α''x''²), where the different values of the single parameter α distinguish the different members. When all members are linearly normalizable, i.e., the following integral is finite irrespective of α, | ||
:<math> | :<math> | ||
\ | -\infty < \; \int_{-\infty}^{\infty} F_\alpha(x) \mathrm{d}x \; < \infty | ||
</math> | </math> | ||
and all members peak around ''x'' = 0, then the family may form a ''delta-convergent sequence''. | |||
===Block functions=== | |||
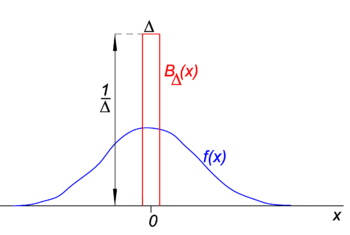
[[Image:Dirac delta.png|thumb|right|350px|Fig. 1. Block function (red) times regular function ''f''(''x'') (blue).]] | [[Image:Dirac delta.png|thumb|right|350px|Fig. 1. Block function (red) times regular function ''f''(''x'') (blue).]] | ||
The simplest example of a delta-convergent sequence is formed by the family of block functions, characterized by positive Δ, | |||
:<math> | :<math> | ||
B_\Delta(x)\equiv | B_\Delta(x)\equiv | ||
| Line 49: | Line 58: | ||
\end{cases} | \end{cases} | ||
</math> | </math> | ||
In Fig. 1 the block function is shown in red. Evidently, the area (width times height) under the red curve is equal to unity, irrespective of the value of Δ, | In Fig. 1 the block function ''B''<sub>Δ</sub> is shown in red. Evidently, the area (width times height) under the red curve is equal to unity, irrespective of the value of Δ, | ||
:<math> | :<math> | ||
\int_{-\infty}^{\infty} B_\Delta(x) \mathrm{d}x = 1 < \infty. | \int_{-\infty}^{\infty} B_\Delta(x) \mathrm{d}x = 1 < \infty. | ||
| Line 62: | Line 71: | ||
</math> | </math> | ||
This shows that the family of block functions converges to the Dirac delta function for decreasing parameter Δ; the family forms a ''delta-convergent sequence''. | |||
'''Note''': We integrated over the whole real axis. Obviously this is not necessary, we could have | '''Note''': We integrated over the whole real axis. Obviously this is not necessary, we could have excluded the positive and negative wings of the block function and integrate only over the hump in the middle, from −Δ/2 to +Δ/2. In mathematical texts, as e.g. Ref. <ref>I. M. Gel'fand and G. E. Shilov, ''Generalized Functions'', vol. 1, Academic Press, New York (1964). Translated from the Russian by E. Saletan.</ref>, this refinement in the integration limits is included in the definition of the delta-convergent sequence. That is, it is required that the integrals over the two wings vanish in the limit. Because the delta-convergent sequences encountered in physical applications satisfy this condition, the integration over the whole real axis is in practice without problems and does not give an extra constraint. Accordingly, we omit the more exact mathematical definition. | ||
===Gaussian functions=== | ===Gaussian functions=== | ||
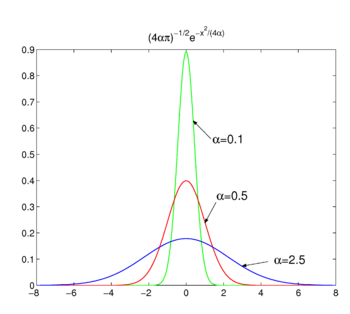
[[Image:Gauss functions for three different parameters.png|thumb| | [[Image:Gauss functions for three different parameters.png|thumb|right|350px|Fig. 2. Gaussian functions.]] | ||
Consider the family, | Consider the family, | ||
:<math> | :<math> | ||
| Line 73: | Line 82: | ||
\int_{-\infty}^\infty F_\alpha(x)\mathrm{d} x = 1. | \int_{-\infty}^\infty F_\alpha(x)\mathrm{d} x = 1. | ||
</math> | </math> | ||
As is shown in Fig. 2 the functions peak around ''x'' = 0 and become | As is shown in Fig. 2 the functions peak around ''x'' = 0 and become narrower for decreasing α. Hence the family of Gaussian functions forms a delta-convergent sequence, | ||
:<math> | |||
\lim_{\alpha \rightarrow 0} F_\alpha (x) \rightarrow \delta(x). | |||
</math> | |||
==References== | ==References== | ||
<references /> | <references /> | ||
Revision as of 08:31, 22 December 2008
In physics, the Dirac delta function is a function introduced by P. A. M. Dirac in his seminal 1930 book on quantum mechanics.[1] Heuristically, the function can be seen as a generalization of the Kronecker delta from integral (elements of ) to real (elements of ) indices.
Note that the Kronecker delta acts as a "filter" in a summation:
In analogy, the Dirac delta function δ(x−a) is defined by (replace i by x and the summation over i by an integration over x),
The Dirac delta function is not an ordinary well-behaved map , but a distribution, also known as an improper or generalized function. Physicists express its special character by stating that the Dirac delta function makes only sense as a factor in an integrand ("under the integral"). Mathematicians say that the delta function is a linear functional on a space of test functions.
Properties
Most commonly one takes the lower and the upper bound in the definition of the delta function equal to and , respectively. From here on this is assumed.
The physicist's proof of these properties proceeds by making proper substitutions into the integral and using the ordinary rules of integral calculus. The last property is the analogy of the multiplication of two identity matrices,
Delta-convergent sequences
There exist families of regular functions of which the family members differ by the value of a single parameter α. An example of such a family is formed by the family of Gaussian functions Fα(x) = exp(−αx²), where the different values of the single parameter α distinguish the different members. When all members are linearly normalizable, i.e., the following integral is finite irrespective of α,
and all members peak around x = 0, then the family may form a delta-convergent sequence.
Block functions
The simplest example of a delta-convergent sequence is formed by the family of block functions, characterized by positive Δ,
In Fig. 1 the block function BΔ is shown in red. Evidently, the area (width times height) under the red curve is equal to unity, irrespective of the value of Δ,
Let the arbitrary function f(x) (blue in Fig. 1) be continuous (no jumps) and finite in the neighborhood of x=0. When Δ becomes very small, and the block function very narrow (and necessarily very high because width times height are constant) the product f(x) BΔ(x) becomes in good approximation equal to f(0) BΔ(x). The narrower the block the better the approximation. Hence for Δ going to zero,
which may be compared with the definition of the delta function,
This shows that the family of block functions converges to the Dirac delta function for decreasing parameter Δ; the family forms a delta-convergent sequence.
Note: We integrated over the whole real axis. Obviously this is not necessary, we could have excluded the positive and negative wings of the block function and integrate only over the hump in the middle, from −Δ/2 to +Δ/2. In mathematical texts, as e.g. Ref. [2], this refinement in the integration limits is included in the definition of the delta-convergent sequence. That is, it is required that the integrals over the two wings vanish in the limit. Because the delta-convergent sequences encountered in physical applications satisfy this condition, the integration over the whole real axis is in practice without problems and does not give an extra constraint. Accordingly, we omit the more exact mathematical definition.
Gaussian functions
Consider the family,
As is shown in Fig. 2 the functions peak around x = 0 and become narrower for decreasing α. Hence the family of Gaussian functions forms a delta-convergent sequence,


![{\displaystyle \sum _{i=m}^{n}\;f_{i}\;\delta _{ia}={\begin{cases}f_{a}&\quad {\hbox{if}}\quad a\in [m,n]\subset \mathbb {Z} \\0&\quad {\hbox{if}}\quad a\notin [m,n].\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d423840356e3321bcaf55a6694917325439011a7)
![{\displaystyle \int _{a_{0}}^{a_{1}}f(x)\delta (x-a)\mathrm {d} x={\begin{cases}f(a)&\quad {\hbox{if}}\quad a\in [a_{0},a_{1}]\subset \mathbb {R} ,\\0&\quad {\hbox{if}}\quad a\notin [a_{0},a_{1}].\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/afb48bb90df31264053453233a5fcd22dba38ea8)